Time plays a central role in our understanding of human error and system failure. Without a detailed knowledge of the flow of events, investigators cannot hope to arrive at accurate and well founded conclusions about the causes of major accidents. This paper argues that existing approaches, such as time lines and fault trees, cannot capture the sequencing and synchronisation constraints that characterise complex human-machine failures. We, therefore, present requirements for future accident modelling techniques that will capture the temporal properties of accidents.
Accidents do not simply 'happen'. They, typically, have complex causes that may take days, weeks or even years to develop (Reason, 1990). Engineers have developed a range of tools and techniques that can be used to represent and reason about these causes of major accidents (Leveson, 1995) For example, time-lines and fault trees have been recommended as analysis tools by a range of governmental and regulatory bodies. Unfortunately, these well established techniques suffer from a number of limitations. In particular, they cannot easily be used to represent and reason about the ways in which human error and systems failure interact during complex accidents (Hollnagel, 1993). More recently, a range of semi-formal and formal notations have been applied from the field of software engineering to support accident analysis. These have ranged from graphical notations, such as Petri Nets (Johnson, 1995) to textual formalisms, including first order logic (Johnson, 1996). Large amounts of commercial, regulatory and governmental funding have been provided to develop a number of case studies in the application of these novel notations (Johnson, 1997a). This paper reviews the insights gained from these case studies. In particular, it is argued that these novel approaches also suffer from serious limitations as tools for modelling the temporal properties of human 'error' and systems 'failure'.
Figure 1 illustrates the way that accident reports help to communicate the findings of accident investigations. After an accident occurs, forensic scientists, engineers and human factors analysts conduct an enquiry into the probable causes of any failure. These causes are then documented in a final report which is distributed to commercial, governmental and regulatory organisations. These documents are intended to influence the design and implementation of similar systems. They are published with the aim of preventing future accidents. Unfortunately, if companies cannot use these reports in an effective manner then previous weaknesses may continue to be a latent cause of future failures.
A number of factors make it difficult to produce clear and consistent accident reports. Accident reports contain the work of many different experts. Forensic scientists, metallurgists, meterologists as well as software engineers and human factors experts all present their findings through these documents. Their conclusions are, typically, separated into a number of different chapters. This has important consequences for the 'usability' of the resulting documents. It can be difficult to trace the ways in which system 'failure' and operator 'error' interact over time. Readers must trace the ways in which the events described in one chapter interact with those mentioned in other sections of the report. For example, the Air Accident Investigation Branch's (1990) report into the Kegworth accident contains a section on the Engine Failure Analysis and another on the Crew Actions. Many of the events that are mentioned in the first chapter are not presented in the second and vice versa. This makes it difficult to trace the exact ways in which equipment failures complicated the task of controlling the aircraft (Johnson, 1994, 1995).
The poor level of integration between human factors and systems analysis can partly be explained by the lack of any integrated tools. For example, the United States' Department of Energy Standard for Hazard Categorisation and Accident Analysis (DOE-STD-1027-92) identifies a number of techniques that can be used to support accident analysis. These include Hazard and Operability Studies (HAZOPS), fault trees, probabilistic risk assessments and Failure Modes, Effects and Criticality Analysis (FMECA). None of these approaches provides explicit means of representing human factors 'failures'.
There are a number of further reasons why previous approaches cannot easily be used to model the events leading to recent accidents. The first is that many techniques, including timelines and Fault Trees, provide only limited means for reasoning about concurrency. This is an important limitation; the increasing integration of both production processes and control technology make it increasingly likely that major accidents will involve simultaneous failures in many different areas of a complex system. Other problems relate to the way in which existing notations support the group processes involved in the generation of an accident report. As mentioned, these documents are, typically, produced by heterogenous teams. The members of these groups often have different backgrounds and training. In consequence, those areas of a timeline that interest one individual may not be of interest to another. Even more seriously, the conclusions of one analyst about the probable ordering of events need not accord with those of another. For example, we shall see that the Fire Service and Ambulance accounts of the Clapham rail crash differ in several important respects (Love and Johnson, 1997). Existing techniques, such as time lines or Fault trees, and novel approaches, including Petri Nets and logics, provide little or no support for identifying and resolving these inconsistencies. In consequence, many accident reports contain incomplete and contradictory information about the sequencing of human error and systems failure.
This paper presents a list of requirements for the temporal modelling of accident sequences. Like Green's (1989) earlier work on the cognitive dimensions of notations, our criteria should be thought of as heuristic. They are derived from experience in modelling a large number of complex accidents. The list is non- exhaustive. We welcome further criteria to guide the development of future modelling techniques. It is important to emphasise, however, that these criteria must not simply focus upon the expressive power of the notation for capturing temporal properties of interaction. In contrast, our criteria also reflect the importance of the usability of the notation itself. It must be possible for practising engineers to learn the new notation in an incremental fashion that reduces the number of errors both in the construction and comprehension of an accident model. Other criteria reflect the importance of groupwork. It must be possible to represent and view particular perspectives on the causes of an accident. It must also be possible to identify any inconsistencies between those perspectives, for instance between the timings given in human factors and systems engineering accounts.
Section 2 develops the argument that existing modelling techniques cannot easily be used to represent and reason about the complex temporal properties of human error and systems failure. In particular, problems are identified for time-lines, fault trees, Petri Nets and first order logic. Section 3, therefore, presents a number of requirements that must be satisfied by any future notation that is to be used to represent complex sequences of operator 'error' and system 'failure'. This section focuses upon temporal expressiveness. In contrast, Section 4 focuses more narrowly upon usability requirements for temporal notations. It is of little benefit developing a notation that can capture a range of both real and relative time properties if it cannot be used by teams of accident investigators. Section 5 presents the conclusions that can be drawn from our work. Areas for future research are also identified.
This section argues that a number of limitations restrict the utility of existing notations as a means of representing and reasoning about the temporal properties of major accidents.
Time-lines are one of the simplest means of representing the flow of events during major accidents. Each critical incident is mapped to a point on a line which starts from the earliest incident in the accident and finishes at the last moment that is considered to be important to the analysis. Figure 2 presents a timeline for some of the events leading to a collision that was reported by the United States Coast Guard (1995). Here we can see the strong visual appeal of this linear notation. Readers can easily gauge the intervals between events because there is a simple relationship between linear distance and the temporal intervals between events. In other words, standard units of distance are used to represent standard units of time. In Figure 2, this is used to indicate the interval between the Ymitos' departure at 09:25 and the immediate events before the collision at 20:40.
Figure 2 represents both the strengths and the weaknesses of timelines as a means of representing the temporal properties of human 'error' and systems 'failure'. The simple relationship between spatial locations on the diagram and temporal locations during an accident has already been noted. The practical consequence of this is that analysts need minimal training to use these models. They can be used as a common medium of communication between the diverse disciplines involved in accident investigations. Unfortunately, there are a number of weaknesses. Figure 2 illustrates the 'uneven' distribution of events over time. Nothing significant is shown to happen between the departure of the Ymitos and the Noordam's entry into the Safety Fairway. Conversely, a large number of critical events take place in the interval between 17:45 and 20:42. The concentration of critical events crams many different annotations into a small area of the line. This reduces the tractability of the resulting timeline. Of course, it is possible to alter the scale so that more space is made available during the immediate run-up to an accident. This, however, ruins the simple, linear relationship between space and time that is claimed to be the key strength of the timeline notation. Initial tests have shown that the consequent use of different temporal granularities leads to considerable comprehension problems for analysts who must ignore spatial clues and refer to the interval markings on these 'distorted' timelines (Johnson, 1997).
Faults trees provide means of avoiding the crowding associated with timelines. This is achieved by using two dimensions to represent the flow of events. Horizontal space is used to represent concurrency. Vertical space is used to represent sequence. Figure 3 illustrates this approach using the syntax recommended by the U.S. Nuclear Regularity Commission's, 'Fault Tree Handbook' (Vesely, Goldberg, Roberts and Haasl, 1981). Basic events, shown as he leaves of the tree, can be used to represent the underlying failures that lead to an accident (Hollnagel, 1993). In Figure 3, the event labelled 'A wiring error has been made...' is true as the result of a conjunction initial events. There are a range of important differences that distinguish the use of accident fault trees from the more conventional application of circuit diagrams to design. These relate to the semantics of the gates that are used to construct the diagrams. Conventionally, the output from an AND gate is true if and only if all of its inputs are true. Accidents cannot be analysed in this way. For example, Figure 3 shows that the hardware error was the result of six events. In a 'traditional' fault tree the error would have been prevented if interface designers or systems engineers had stopped any one of these events from happening. In accident analysis, however, there is no means of knowing if an accident would actually have been avoided in this way. An accident may still have occurred even if only one or two of the initiating events occurred. In this context, therefore, an AND gate represents the fact that an accident report cites a number of initiating events as contributing to the output event. No inferences can be made about the outcome of an AND gate if any of the initiating events do not hold.
The main criticism of fault trees is that they provide an extremely impoverished representation of time. There is no ordering amongst the events that lead into a gate. A simple linear sequence is assumed to hold between gates and the events lower down in the tree. The U.S. Nuclear Regulatory Commission have, therefore, proposed PRIORITY-AND gates as a means of capturing temporal properties of interaction (Vesely, Goldberg, Roberts, Haasl, 1981). Sequential constraints are shown inside an ellipse drawn to the right of the gate. The gate event is not true unless the ordering is followed. Unfortunately, real-time is not supported. This is significant because precise timings can have a critical impact upon an operator's ability to respond to a critical incident. Our previous work, therefore, extended the fault tree notation to include real-time (Love and Johnson, 1997). This is illustrated in Figure 4. Approximate timings from the Clapham railway accident are shown in the left hand corner of each event. The annotation in the right hand corner provides evidence for the timing information by citing a paragraph and page reference in the accident report.
A number of limitations still affect the extended notation shown in Figure 4. It is difficult to represent the conflicts that often arise in the timings that are available after complex accidents. For example, the London Ambulance Service records state that the first call from the London Fire Brigade was received at 08:16. London Fire Brigade records state that the call was made at 08:19. Clearly such timing differences may have a profound impact when one is analysing the response times of different emergency organisations. Similarly, Figure 4 assumes that all of the events contributing to a gate are presented in temporal ordering from left to right. Driver Keating's observations are claimed to have occurred before Driver Preston's. However, it is difficult to sustain this approach for more complex temporal relationships. It is unclear how to represent events that extend over several points in time. As with timelines, this problem might be overcome through ad hoc annotations. This would increase the complexity of the notation.
Petri nets have been specifically developed to represent the complex sequencing and synchronisation constraints that cannot easily be captured by fault trees and time lines. Figure 5 shows how a Petri net can represent the events leading up to an accident. In this case, we have shown the lead up to the Kegworth air crash (AAIB, 1990). The filled in circles represent tokens. These 'mark' the unfilled circles, or places, that represent assertions about the state of the system. In this diagram, places are marked to show that there are vibrations in the number 1 engine and that there is smoke. An important benefit of the Petri Net notation is that analysts can simulate the flow of events in an accident model by altering the markings in a network. This is done through an iterative process of marking and firing. If all of the places leading to a transition, denoted by the rectangles, are marked then that transition can fire. In Figure 5, the transitions labelled 'Smoke enters ventilation' and 'Sensors begin to detect vibration' can fire. All of the output places from this transition will then be marked. For example, if the place labelled 'Sensors begin to detect vibration' fired then the place 'AVM is displaying an out of range reading' would be marked.
A number of limitations complicate the application of Petri nets to analyse accidents that involve interactive systems. In particular, they do not capture 'real' time. Various modifications have been applied to the classic model. Levi and Agrawala (1990), use 'time augmented' Petri nets to introduce the concept of 'proving safety in the presence of time'. Unfortunately, even if someone can understand the complex firings of a 'time augmented' Petri net, they may not be able to comprehend the underlying mathematical formulae that must be used if diagrams, such as Figure 5, are to be used to analyse human 'error' and system 'failure' (Palanque, Paterno, Bastide and Mezzanotte, 1996).
"The No.1 engine suffered fatigue of one of its fan blades which caused detachment of the blade outer panel. This led to a series of compressor stalls, over a period of 22 seconds until the engine autothrottle was disengaged.'' (AAIB, 1989, Finding 19, page 144)
From this it is possible to identify two systems problems; a fan-blade fractured and there were compressor stalls in the number one engine. Unfortunately, it is not possible to identify which of the fan-blades actually failed from the previous quotation. Readers must search through earlier sections of the report to find this information:
"Since blade No.17 was the only fan blade to have suffered serious fatigue, it was concluded that the initiating event for Event 2 must have been the ingestion by the fan of a foreign object.'' (AAIB, 1989, page 115).
Logic provides a means of combining the facts that are embodied within these natural language statements. The intention is to provide a common framework that can be used to describe the events that led to the failure. This reduces the burdens that are associated with cross-referencing the many different sections of a report:
fracture(no_1_engine, fan_blade_17). [1] stall(no_1_engine, compressor). [2]Logic has also been used to represent more human-centred causes of major accidents. For example, the following clause represents some of the cognitive factors that influenced a critical decision during the Kegworth accident (Johnson, 1998). A drop in vibrations once the right engine was idled helped to strengthen the First Officer's assessment that there was no fire in the left engine. It is important to notice that one of the grounds for assuming that the left engine is not on fire, is the First Officer's belief that the right engine is on fire:
know(first_officer, not fire(left_engine)) <= display(avm, left_engine, normal), know(first_officer, fire(right_engine)). [3]Unfortunately, there is no notion of time or sequence in first order logic. The display may present the 'normal' reading many days after the operator diagnosed the fire in the right engine. This is clearly not what the analyst intended. Temporal logic operators, such as O (read as 'next'), [] (read as 'always') and <> (read as 'eventually'), can be introduced to make the timing information explicit within the previous clause (Johnson, 1996). The operator believes that the right engine is on fire immediately after the display for the left engine has returned to normal:
know(first_officer, not fire(left_engine)) <= display(avm, left_engine, normal), O know(first_officer, fire(right_engine)). [4]Temporal logic provides a textual representation of the timing properties that are represented using the graphical and spatial cues of time lines. Similarly, the knows predicate mirrors the informal labels, such as 'Captain is unfamilliar with the ventilation' in Petri Nets. Such similarities further complicate the designers' task in identifying a suitable notation for accident analysis. They illustrate the need to find more specific criteria than 'the ability to represent time'. The following section, therefore, presents a more detailed set of requirements for the temporal modelling of human 'error' and system 'failure'.
A principle requirement for any accident modelling notation is that it should be capable of representing both human 'error' and system 'failure'. This creates problems because the temporal properties of control systems are very different from those of their operators. For example, the Cullen report into the Piper Alpha disaster contains the following observations (Department of Energy, 1990):
"Mr Clark stated that he left the maintenance office within 1 or 2 minutes of the tannoy call. He ran down so as to reach the Control Room before Mr Savage rang through. He estimated that his journey down to the Control Room would take 2-3 minutes. He stated that he had just arrived and was about to start on the red tags when Mr Savage rang in..." (page 73).
This can be contrasted with the following observations about system behaviour within the same report. Here the focus is upon the observable behaviour of a gas detection system during the disaster:
"It became apparent that only the larger leaks could give a flammable gas cloud containing the quantity of fuel evidently necessary to cause the observed explosion effects. Interest centred therefore particularly on series 42, which was the only test at a leak rate of 100 kg/min. In this test the low level alarms occurred first for C3 in 5 seconds, then for C2, C4 and C5 in 15, 20 and 25 seconds respectively..." (page 77).
The first quotation is based around an individual's recollections. The timings are vague and, in this case, difficult to substantiate. The second quotation provides clear and precise timings for alarms that have been validated by empirical studies on replicas of the system. This section, therefore, argues that there are a range of temporal properties that must be captured by any notation that is to support accident modelling. In particular, these properties do not simply relate to the real and interval time distinctions that have typified previous discussions of temporal modelling in fields such as Artificial Intelligence (Allen, 1984) and concurrency theory (Coulouris, Dollimore and Kindberg, 1994). They relate to the nature of the evidence that supports temporal information. Some timings may be well grounded while other temporal information may be vague and imprecise. It is also important to consider the ways in which subjectivity will affect the analysis of human 'error' and systems 'failure'. For instance, analysts from different disciplines often disagree about the moment at which an accident actually begins. Similarly, it can be non-trivial to identify the time at which an accident finishes.
When does an accident begin? This is a non-trivial question. For example, the Clapham Railway crash began when Driver Keating mistakenly thought that an unusual change in signals was a message from the signalman rather than the result of a wiring error (Department of Transport, 1989). Alternatively, the accident might have started when the initial wiring fault was introduced into the circuit. Equally, it might have been when the signalling engineer was trained how to inspect the safely of their repairs. The key point here is that the starting point for an accident is often a subjective decision that reflects the analyst's view of its causes. Accident modelling notations must, therefore, represent this subjective decision. It must be possible for readers to clearly identify the moment at which an analyst considers an accident to begin. A related question is 'when does an accident end?'. Fault trees typically stop at the 'undesired event'. In accident reports, events after the accident are also important. These, typically, include the operator actions that are taken to mitigate the effects of system failure. For example, the Ambulance service played an important part in the Clapham accident. Although their actions did not cause the accident, they contributed to the saving of lives. They reduced the consequences of human 'error' and system 'failure'. Figure 6 illustrates how fault trees can be extended both above and below a critical incident. The accident is at the centre of the tree. The roots below the tree represent the causes. The leaves above the centre represent the events following the accident. The analyst's view of the start and finish of the accident are explicitly bounded by the extent of the tree.
This diagram illustrates the way in which post-accident sequences stem from the collision. As can be seen, no gates are used after the central event. This reflects the certain, causal flow from the consequences of the collision. Figure 6 illustrates both the strengths and the weaknesses of fault trees. The lines between nodes represent causal, temporal and logical relationships amongst the events leading to and from an accident. This overloading provides considerable expressive power. It can also be misleading.
Figure 7 illustrates the structure of many accident reports. Each chapter presents a chronology of events from a different perspective. As a result, if a reader wants to build up a coherent view of all of the events in an accident at a particular point in time then they are forced to cross-reference many different sections of the report. For example, the events occurring at times T1 and T2 are described in each of the chapters represented in Figure 7.
Formal and semi-formal notations can be used to avoid the problems mentioned above. They provide explicit means of representing the concurrent events that occur in different areas of a system. They can also be used to represent the way in system failures and human error might combine, at critical moments, to create the circumstances for an accident. To illustrate the importance of this, consider the following excerpts from the Fennel report into the Kings Cross Underground fire (Department of Transport, 1988):
"20:25 Station Inspector Hayes, Railman Farrell and most of the other London Underground staff left the station via the Midland City subway. 20:41 London Fire Brigade Assistant Chief Officer Kennedy arrived and took on command." (page 56).
"Area Manager Harley was preoccupied for a time with bringing Victoria Line trains through by manual control as the fire had damaged the circuitry which allowed automatic operation. None of the managers appreciate the scale of the disaster above while they were below, and none attempted to contact the emergency services or London Underground personnel on the surface by telephone. When each of them got to the surface by way of the Midland City exit they saw their main task as liason with other London Underground personnel. Traffic Manager Weston, who came up shortly after 20:30 assumed that acting Manager Nelson was in overall charge. He did not make contact with the London Fire Brigade area control unit once he saw that the Incident Officer Mr Green had arrived" (page 73).
These two citations are important because they reveal how details about the same moment in time can be spread across different sections of an accident report. In order to form a coherent account of the movements of London Underground personnel between 20:25 and 20:30, it is not sufficient to read either the synopsis from page 56 or the more detailed account from page 73. The former excerpt records the movements of Station Inspector Hayes and Railman Farrell. The latter report does not mention these individuals but does record the movements of Area Manager Harley and Traffic Manager Weston. Such problems can be avoided by using notations that describe the concurrent movements of these different individuals. For example, Figure 8 presents a Petri Net which synchronises the departure of the various London Underground personnel mentioned in both extracts. It uses information that is spread throughout the linear structure of the official report to construct a model of the events leading to the evacuation of part of the Underground station. Concurrency is represented because once the transition labelled 'Area Manager Harley decides to evacuate all remaining staff' fires, then the subsequent places will all be marked. This indicates that Harley, Hayes and Farrell are all exiting through the Midland City Line.
There are a number of limitations with the previous diagram. In particular, the accident report does not indicate that all personnel evacuated the site at exactly the same time. This need not be a significant limitation; the accident report simply does not give us enough information to discriminate between the moment that the various personnel chose to leave. More significantly, however, Figure 8 only captures the relative timings of various events. The evacuation procedure took place after Area Manager Harley's decision to evacuate. This, in turn, occurred after he had checked to make sure that the platforms were clear of passengers. What the previous diagram does not represent is the real-time at which these different events occurred. This is a significant limitation. A minutes delay can literally make the difference between life and death during a major fire. It is, therefore, important that accident models capture both real and relative temporal constraints.
The previous section has made the case that accident modelling notations must be capable of representing the real-time properties of human 'error' and system 'failure'. It is important, however, to emphasise that this must not force analysts into undue commitment when the exact timing for an event is unknown. For example, the Cullen report into the Piper Alpha accident contains the following passage (Department of Energy, 1990):
"(Mr Grieve) was unaware that PSV 504 had been removed; he learnt this only when he was in hospital after the disaster. Mr Grieve was uncertain exactly when he overheard Mr Bollands' first call to Mr Richards. He was also unsure how much time elapsed before he went down; his estimates ranged up to ten minutes. He may have arrived at the condensate pumps some 2-3 minutes before the initial explosion" (pages 85-86)
This citation is important because it re-iterates the uncertainty that operators may often express about the exact sequence of events leading up to an accident. This uncertainty typifies the stress, anxiety and guilt that are often felt in the aftermath of a tragedy. In consequence, even with sophisticated logging techniques it may not be possible to associate particular events with particular moment in time. Some notations provide more support for the representation of this lack of evidence than others. For example, timelines may be extended with informal annotations as shown in Figure 9.
The annotations below the timeline are used to indicate the position of events whose time is known, either through corroborated eye witness statements or through external monitoring of the event. In contrast, the annotations above the line are used to indicate imprecise or unsubstantiated timings. The lines from the label 'Mr Grieve arrives at the condensate pumps, 2-3 minutes before the initial explosion' are used to indicate that we do not know when exactly Mr Grieve's left in the interval between 21:57 and 21:58. Similarly, the timeline in Figure 9 does not record exactly when three maydays were sent between 22:04 and 22:08. Nor does it record the exact moment when each of the 22 survivors left between 22:01 and 22:20.
The previous paragraph has argued that timelines can represent events whose exact timings are unknown. This is achieved by denoting an interval during which the event is assumed to have taken place. In contrast, many accidents are caused by human 'errors' and systems 'failures' that develop over an interval of time whose bounds are well defined. There is an important distinction between this sort of information and that shown above the timeline in Figure 9. In the former case the event is instantaneous but it's timing is not known, in the latter case the property is continuous and its duration is well known. This distinction could be supported by introducing further annotations within the timeline notation. For example, Figure 10 shows how a high pressure gas fire continued from the rupture of the Tartan riser at 22:20.
Figure 10 illustrates the way in which additional syntactic features must be introduced if graphical notations are to represent important distinctions between timing constraints. In this instance, imprecise information must be handled differently from the precise timings of continuous properties. These additional syntactic features jeopardise the tractability of graphical notations. Textual notations provide alternative means of representing the real and relative timings that characterise human 'error' and systems 'failure'.
Section 2.2 argued that annotations can be used to introduce real-time constraints into Fault Tree diagrams (Love and Johnson, 1997). This does not, however, capture the full range of temporal properties that occur in natural language, accident reports. For example, the following citation comes from an Air Accident Investigation Branch report into a helicopter crash near Lochgilphead, Argyll in Scotland:
"The penultimate task was to transfer fish from Loch Glashen to some sea cages off the western shore of Loch Fyne near Tarbert. Before the first transfer, G-PLMA was refuelled to 45% fuel; the commander then picked up the loaded bucket and flew to the sea cages near Tarbert where he discharged the fish. Bringing back the empty bucket, he left this bucket at the fish containers and flew to the refuelling area to replenish again to 45%. This was the procedure for each run and each took between 25 and 40 minutes. The task was expected to take four lifts but seven were required to complete it which resulted in the task taking about one and a half hours longer than planned. The commander started this task at approximately 1645 hrs and completed the first six lifts uneventfully. Part way through this task, at about 1900 hrs, the commander telephoned one of the company managers to say that he had not started the final task and that he would be spending the night in the local area..." (Section 1.1.3, AAIB, 1996).
This extract contains real time observations; the task started at approximately 1645hrs. It contains temporal information that can only be analysed relative to other events; "before the first transfer...". It contains imprecise durations for repeated tasks; "the procedure for each run took between 25 and 40 minutes". It is difficult for formal and semi-formal notations to capture this range of temporal constraints. However, some approaches can represent many of these timings. For example, first order logic can be extended with time points. The commander started his task at 1645:
start_task(commander, 16:45) [6]However, the accident report states that this is an imprecise timing. The commander started their task at approximately 1645hrs. This imprecision can be represented by the use of variables that range over points in time. In the following clause, the temporal variable, t, occurs before 1650hrs but after 1640hrs:
exists t: start_task(commander, t), before(1640, t), before(t, 1650). [7]Using this mix of real-time and temporal variables, it is possible to construct increasingly more complex models of the timings that are given in both eye-witness accounts and the synopses that are constructed within accident reports. For example, the commander telephoned the company manager at some point after starting the task. This occurred around 1900hrs :
exists t,t': start_task(commander, t) , before(1640, t), before(t, 1650), telephone(commander, manager, t'), before(1855, t'), before(t', 1905). [8]A strong benefit of this approach is that it can be used to identify inconsistencies in the temporal information that is presented to boards of enquiry. For example, a contradiction would arise if evidence emerged that the telephone call had taken place after 1905. The previous clause explicitly states that the telephone call took place before 1905hrs. These temporal inconsistencies are a significant weakness of many existing accident reports (Johnson, McCarthy and Wright , 1995).
It is a frequent observation in accident reports that the evidence of one witness does not agree with that of another. Most often, these disagreements focus upon the sequence and timing of critical events. For example, the following citation is taken from the Air Accidents Investigation Branch's (1995) report into a near accident involving a Boeing 737-400:
"From this point there is a divergence in the recollection of the passage of time between the three individuals concerned. The Line Engineer thought that he had handed the job over, moved the Boeing 737-500 aircraft and returned to the Line Engineering area by about 2200hrs. The fitter believed that he went immediately, at about 2140 hrs on the instruction of the Controller, to the aircraft in T2 (hangar) and started to open the cowlings of the Number 2 engine. He then waited until the Controller joined him in T2 before continuing the task. The Controller, however, believed that they both went to T2 together sometime around midnight, after he had spent a considerable time organising Base Maintenance activity for the night with a view to minimising the number of interruptions to the inspection."
The problem here is that analysts are forced not so much to represent uncertainty but to represent at least two different views of the events leading to an accident. The following Petri Nets illustrate this point. In Figure 11 a) the Line Engineer's view is represented. 11 b) shows the Fitter's recollections. Figure 11 c) shows the Base Controller's version of events. The main conflict arises between the Fitter's recollections and those of the Controller. The Fitter suggests that he was already in hangar T2 by 21:40, well before the Controller's arrival. The Controller's account suggests that they both arrived in the hangar together at 24:00.
Petri Nets have not previously been used to represent and reason about such inconsistency. Figure 11 only provides limited help in this respect; analysts must manually inspect the different networks to identify the differences between each individual's account. Figure 12 shows how such inconsistencies might be explicitly represented with the Petri Net notation. A double headed arrow highlights the conflict between the two accounts. Unfortunately, such syntactic extensions increase the complexity of graphical notations. This is a significant issue given that analysts much also remember important differences between places, transitions, tokens and the various real-time extensions to the 'classical' Petri Net notation.
It must be possible for analysts to resolve any inconsistencies that are critical to a clear and coherent understanding of an accident. Where there is contradictory evidence, this involves the skill and judgement of the investigator. However, if analysts do not explicitly represent this 'probable' version of events then it is very likely that individual readers will choose to construct different interpretations of the course of an accident. In our example, some people will choose to follow the Controller's account. Others will choose to believe the Fitter's version of events. Figure 13 illustrates the way in which analysts might avoid this confusion by explicitly representing a 'probable' version of events. It is important to note the annotation to the transition showing the fitter's arrival at T2 indicates that there is contradictory evidence for this portion of the model. Again, without such syntactic extensions, analysts would have no means of identifying well-established observations from assumptions that are made 'on the balance of the evidence'.
The Department of Transport (1987) report into the sinking of the Herald of Free Enterprise lists four areas in which the ship's operating company failed to listen to the complaints, suggestions and wishes of their Masters:
"(a) Complaints that the ships proceed to sea carrying passengers in excess of the permitted number. (b) The wish to have lights fitted on the bridge to indicate whether the bow and stern doors were open or closed. (c) Draught marks could not be read. Ships were not provided with information for reading draughts. At times ships were required to arrive and sail from Zeebruge trimmed by the head, without any relative stability information. (d) The wish to have a high capacity ballast pump to deal with the Zeebruge trimming ballast." (page 17).
The fact that it was possible to carry more than the permitted number of passengers meant that the severity of the incident was increased. The lack of lights to indicate the state of the bow door prevented the bridge from observing whether they were open or closed as they set sail. The lack of draught marks and the absence of ballast pumps prevented the crew from trimming the ship so that water entry was less likely given that the bow doors were open. It is possible to produce a Fault tree diagram to represent the way in which each of these factors contributed to the final accident. This is illustrated in Figure 14.
This diagram only represents some of the managerial problems that led to the accident. The Decision of the court also identified a number of key individuals who were at fault during the disaster:
"The Court, having carefully inquired into the circumstances attending the above-mentioned shipping casualty, find for the reasons stated in the Report, that the capsizing of the HERALD OF FREE ENTERPRISE was partly caused or contributed to by serious negligence in the discharging of their duties by Captain David Lewry (Master), Mr Leslie Sabel (Chief Officer) and Mr Mark Victor Stanley (Assistant bosun), and partly caused or contributed by the fault of Townsend Car Ferries Limited (the Owners)." (Decision of the Court, Department of Transport).
Figure 15, therefore, extends the previous diagram to represent some of the activities of the individuals who were cited in the Department of Transport report. For example, Assistant bosun Stanley opened the bow doors on arrival in Zeebruge, he supervised cleaning and maintenance activities and then went to his cabin where he remained until the Herald began to capsize. It was his duty to close the bow doors at the time of departure from Zeebruge.
Figure 15 does not capture the criticality of the various events under consideration. This is important because events can have a different impact at different times during the course of an accident. For example, Mr Stanley's nap would have had a marginal impact if it had occurred at a time when the ship was safely docked in Zeebruge. Figure 16, therefore, illustrates a graphical extension to the fault-tree notation that can be used to represent criticality. The exact definition of levels of criticality depends upon the application domain (Leveson, 1995). There are, however, some widely accepted definitions. For example, the United States Department of Defence (MIL-STD-882B: System Safety Program Requirements) defines a negligible failure as one that will not result in injury, occupational illness or system damage. A marginal failure may cause minor injury, minor occupational illness or minor system damage. A critical failure causes severe injury, severe occupational illness or major system damage. A catastrophic fault may causes death or system loss.
We can apply these annotations to represent a criticality assessment for the events leading up to the capsize. For instance, the lack of an effective counting system for passengers might be considered a negligible failure because it did not directly lead to loss of life. In contrast, the lack of any effective warning system for the state of the bow doors was a critical event. It is less important to emphasise that Figure 17 represents a subjective classification. It reflects one analysts view of the relative criticality of key events during the course of an accident. Too often these assessments are left as implicit judgements within the natural language of an accident report (Johnson, 1996).
This section argues that accident investigators must consider the usability of modelling notations in addition to their temporal expressiveness.
Austin and Perkin's (1993) survey of four hundred and fourty-four commercial and academic software engineers indicated that 'readability' was a significant barrier to the application of formal notations. The following table presents the percentage of respondents who felt that a particular barrier was a significant problems for the commercial development of these notations:
The specification is not readable by the clients. 23% Some aspects of specification are difficult to define in a mathematical model: timing constraints; HCI; performance; reliability; maintainability; availability... 21% A specification will not model all aspects of the real world: hardware; environment... 19% Lack of experienced staff 18% To use a formal method you have to do proofs which dramatically increases the development time (and hence cost) 16% Development costs increase 15% Mistakes can be made in the specification 14%Austin and Perkin's findings have been confirmed by subsequent empirical work (Johnson, 1997). This suggests that visual appeal is an important determinant in the success or failure of modelling notations. Languages which have a low visual appeal are often rejected, even though they may reduce the number of errors that an analyst makes during the modelling process. This is a serious cause for concern because there are important benefits to be gained from languages that have a relatively low initial appeal. For example, formal reasoning techniques can be used to establish the internal consistency of an accident report. Unfortunately, these techniques are most often supported by textual notations that are often criticised as being less 'readable' than their graphical counterparts. The following clauses illustrate the benefits of these reasoning techniques that would be sacrificed if visual appeal was allowed to obscure the reasoning powers of textual notations. These state that at some time between 20:30 and 20:36, Broekhoven and Veldhoen were performing a navigation radar check and were not correlating radar targets:
exists t :
during(perform(broekhoven, navigation_radar_check), t),
not during(perform(broekhoven, correlate_radar_targets), t),
in(t, 2030, 2036). [10]
exists t :
during(perform(veldhoen, navigation_radar_check), t),
not during(perform(veldhoen, correlate_radar_targets), t),
in(t, 2030, 2036). [11]
Proof techniques can be used to establish the relationship between the evidence presented in an accident report
and the conclusions which boards of enquiry use to draft future legislation. Unless this can be done, it will be
difficult for commercial organisations to understand the reasons why particular sanctions may be imposed in the
aftermath of major accidents (Johnson, 1994). For example, the Coast Guard enquiry made the following
observation about the collision between the Noordam and the Ymitos:
'The proximate cause of the casualty was the failure of Chief Officer Broekhoven, the person in charge of the watch on the NOORDAM at the time of the casualty, to maintain a vigilant watch in that he did not detect the presence of the MOUNT YMITOS visually or on radar until the MOUNT YMITOS was less than 1 mile away, less than 2 minutes before the collision.' [Conclusion 1].
Formal proof techniques can be used to demonstrate that this conclusion is valid given the evidence that is presented in an accident report. For instance, the following clause is derived from Conclusion 1 in the Coast Guard report:
forall t:
not during(vigilant(broekhoven), t) <=>
(not during(observe(broekhoven, mount_ymitos, visual), t),
before(t, 2040)),
(not during(observe(broekhoven, mount_ymitos, arpa_radar), t),
before(t, 2040)).
[12]
In order to justify Conclusion 1 we must consider two different cases. The first concerns the reasons why
Broekhoven failed to make visual contact with the Mount Ymitos. The second addresses the failure to detect
the Ymitos using the ARPA radar. In order to establish the connection between the conclusion and the
evidence presented in the body of the report it is necessary for analysts to explicitly state the reasons supporting
particular findings. For example, one of the reasons why Broekhoven failed to observe the Mount Ymitos was
that he used the radar for navigation and not for collision avoidance:
forall t: not during(observe(broekhoven, mount_ymitos, arpa_radar), t) <= during(perform(broekhoven, navigation_radar_check), t), not during(perform(broekhoven, correlate_radar_targets), t). [13]We can now prove that the second part of our formalisation of Conclusion 1 is satisfied by the evidence in the accident report. This can be done by applying the following inference rule to [10] and [13].
forall t: P(t) => Q(t), exists t': P(t') |- exists t': Q(t') [14]Informally, this argument can be expressed as follows. From clause [13], we conclude that Broekhoven failed to observe the Mount Ymitos using the ARPA radar during any interval in which he was performing a navigation radar check and did not correlating radar targets. From clause [10] we know that know that Broekhoven was performing a navigation radar check and was not correlating radar targets between 20:30 and 20:36. Clause [14] tells us that if, we have clause [13] and clause [10] we can infer that Broekhoven failed to observe the Mount Ymitos using the ARPA radar during the interval between 20:30 and 20:36.
The previous proof illustrates a weakness in the accident report. Our formalisation of Conclusion 1 stated that Broekhoven did not observe the Mount Ymitos using the radar until 20:42. Our model has been used to prove that Broekhoven was pre-occupied with navigation checks between 20:30 and 20:36. This leaves at least six minutes unaccounted for. During that time, Broekhoven began turning the Noordam to the North. The accident report makes no reference to the use of the ARPA during this interval. The reader has to assume that the system was not used during this or subsequent operations prior to the collision at 20:42. Such findings are significant because they have important consequences for the recommendations that might be drawn from the report. For example, it is normal practice for officers to correlate radar targets when approaching an unfamiliar port. In the interval from 20:30 to 20:36 we can clearly see that navigation problems explain why Broekhoven did not perform these checks. We cannot, however, explain the omission during the final six minutes before the collision.
The critical point here is not that there are errors in a particular report nor even that formal proof techniques can be used to identify those flaws. It is, rather, that analysts must carefully weigh the benefits of visual appeal against potential costs in terms of the reasoning power of the notation. This does not imply that all proof techniques lack visual appeal. For example, Figure 18 illustrates the use of Conclusion, Analysis and Evidence (CAE) diagrams to provide a graphical representation of the textual reasoning process shown in previous clauses. Broekhoven failed to maintain a vigilant watch. This is supported by [Conclusion 1] in the report and is formalised in clause [12]. The conclusion relies upon an analysis which suggests that Broekhoven did not use the radar effectively. In this analysis, he was preoccupied with navigation rather than collision avoidance, from [Paragraph 39] represented in clause [13]. This is supported by evidence in [Paragraph 39]. A similar proof process can be conducted to establish the reasons why Broekhoven failed to make visual contact before 2037hrs, see (Johnson, 1997a).
Different notations offer different degrees of support to various stages of the learning process. For instance, graphical notations may be easier for novices to understand than textual notations. Features such as a simple linear relationship between time and the position of annotations on a diagram can help people at the lower ends of the learning curve to focus upon key concepts rather than underlying mechanisms. Conversely the more advanced features of temporal logic, such as model based semantics and Kripke proof techniques, help more experienced analysts to exploit the full power of the language. However, analysts will not exploit the more advanced features of a temporal notation unless they can be persuaded of its benefits. Carroll (1992) reiterates this point when he argues that training costs must be carefully balanced against the perceived benefit of using the formalism. Analysts must be enabled to perform basic tasks with only a cursory training. This may involve the provision of support tools or learning environments just as training wheels are provided when we first learn to ride a bike. More advanced tasks should involve proportionally more effort. At this stage the training wheels may be removed and the analysts is freed to explore the full power of the approach. Although this idea has had considerable impact upon interface designers, it has had almost no impact upon the developers of temporal notations (Johnson, 1998).
It might be argued that analysts should recruit different notations for modelling the different temporal characteristics of human 'error' and systems 'failure'. Previous citations from the Cullen report into the Piper Alpha disaster can be used to illustrate this point (Department of Energy, 1990). Here is part of the human factors account of the failure:
"Mr Clark stated that he left the maintenance office within 1 or 2 minutes of the tannoy call. He ran down so as to reach the Control Room before Mr Savage rang through. He estimated that his journey down to the Control Room would take 2-3 minutes. He stated that he had just arrived and was about to start on the red tags when Mr Savage rang in..." (page 73).
This can be represented by the following Petri Net. The decision to use this graphical formalism is justified because the timings provided by Mr Clark are approximate. The use of time-points in a logic notation commits the analysts to specific intervals, see Section 3.3. This would require further corroboration of Mr Clark's testimony. In contrast, Figure 19 simply captures the remembered sequence that was presented to the court of Inquiry.
The previous human factors citation can be contrasted with the following excerpt from the systems analysis. Simulations helps the analyst to be more confident about the timing of events:
"It became apparent that only the larger leaks could give a flammable gas cloud containing the quantity of fuel evidently necessary to cause the observed explosion effects. Interest centred therefore particularly on series 42, which was the only test at a leak rate of 100 kg/min. In this test the low level alarms occurred first for C3 in 5 seconds, then for C2, C4 and C5 in 15, 20 and 25 seconds respectively..." (page 77).
Empirical evidence provides a greater degree of certainty about the impact of particular gas flows upon the alarm system. This additional certainty is often a feature of systems analysis, as opposed to the more subjective recollections of system operators, might best be represented using time points in first order logic. Instead of representing timings as annotations to Petri Nets, this approach integrates the more certain timing information into the formalisation:
exists t: leak_rate(100, t) => alarm(C3, t+5), alarm(C2, t+15), alarm(C4, t+20), alarm(C5, t+25) [15]Unfortunately, the close interaction between human 'error' and systems 'engineering' makes it imperative that some unifying formalism is provided. For example, the physical characteristics of the detection equipment, mentioned in the previous quotation, had a profound impact upon the amount of time that was available for operators to respond to the developing disaster. This point is made explicit in the following citation from the Piper Alpha report:
"The other person in the Control Room was Mr Clark. He said that he was unaware of the 2 centrifugal compressors tripping but he did experience the first low gas alarm... " (page 74).
It is difficult to obtain a clear overview of the events leading to failure if system characteristics cannot be directly linked back to the impact that they had upon the operators. Figure 20 illustrates how this integration can be achieved using Petri Nets. Mr Clark's recollections suggest that he noticed the warning indicated by the C3 low level alarm which occurred five seconds after the gas flow exceeded 100kg/min. It should be noted that this Petri Net does not specify the exact mechanism by which Mr Clark was informed of the alarm. His recollections suggest that another operator, Mr Bolland, informed him of the warning. He may also have noticed an alarm on his display matrix.
It is important to emphasise that the integration shown in Figure 20 is unsatisfactory. The nature of the systems engineering evidence is qualitatively different from that of the human factors account. In the former case, repeated empirical measures can be made on simulations to confirm the timing of gas flows to alarm signals. In the latter case, operator recollections of high-stress situations are used to annotate timing characteristics. I am unaware of any existing notation that can be used to satisfactorily integrate human factors and systems account and which provides a means of representing the evidence which justifies those observations. The Conclusion, Analysis, Evidence diagrams that were introduced in the previous section, go part of the way to achieving this objective. There are, however, may problems. In particular, they focus upon particular lines of argument and the evidence that supports those arguments. They do not provide a timeline in the manner shown by the Petri Net in Figure 20. Alternatively, Figure 20 could be further annotated to indicate the degree of certainty about human factors and systems engineering observations. This would, in turn, have a significant impact upon the usability of a complex notation that has already been extended with temporal annotations.
The use of a formal or semi-formal notation does not guarantee that an accident model will be free from mistakes. These languages often have complex syntactical rules which must be followed if the resulting descriptions are to be understood by other users. It is, therefore, important that we provide as much support as possible during the construction of accident models. Figure 21 illustrates the user interface to Logica's commercial Z tool, called formaliser. Z extends first order logic with techniques for structuring large scale specifications. It has also been used both for interface design (Johnson, 1995a) and accident analysis (Botting and Johnson, 1998). The important point about this tool is that it automatically helps designers to construct syntactically correct specifications through structure editing. Analysts can select frequently used concepts and the system will automatically insert the appropriate syntax into the model. The analyst then only has to modify the names of appropriate terms, functions etc. Type checking tools can then be used to ensure that the variable names are appropriate for the context in which they appear. Similar tools exist for the construction of both Petri Nets and Fault Trees (Johnson, 1995). Without such support, it is difficult to conceive of large teams of designers constructing and maintaining 'realistic' models of complex accidents. It is important to note, however, that few of these tools provide explicit support for the development of temporal specifications.
Other tools can be used to 'directly' develop prototype implementations from formal specifications (Johnson, 1996). This is important because mathematical specification techniques can provide an extremely poor impression of the events leading to an accident. Interactive simulations can be shown to other analysts in order to validate the assumptions that are contained within accident models. For example, the following excerpt is taken from the Air Accidents Investigation Branch's (1995) report into a near accident involving a Boeing 737- 400:
"After he (the shift leader) had returned to the Line Office, he was informed of the aircraft fuel load for the sector and sent one of the Line Engineering staff to supervise the refuelling and give the aircraft the pre-departure check for the first flight of the day." (Section 1.1.3, paragraph 2).
This brief citation can be used to illustrate simulation techniques for accident modelling. The following clauses use the syntax supported by the Prolog logic programming environment to represent the events described in the accident report. Note how an integer 'time' value is used to encode the sequencing information that is implicit in the natural language account. As mentioned, there is no notion of time in classical first order logic and so analysts must introduce some means of representing the flow of events in an accident report. The additional overhead of manually including such event counters can be reduced by using temporal logic simulation environments (Johnson, 1996):
time(1, position(shift_leader, line_office)). time(2, inform(_, shift_leader, sector_fuel_load)). time(2, inform(shift_leader, line_engineers, supervise_refuel)). time(2, inform(shift_leader, line_engineers, perform_departure_checks)).Analysts can use logic programming environments, such as Prolog, to simulate the events in an accident report. For example, meta-predicates can assert and retract the facts that are known about particular individuals and systems during the course of an accident (Dhillon, 1997). In its most advanced form, this approach can be used to generate the displays that operators actually saw during the course of a failure (Johnson, 1996). This provides a unique means of gaining further empirical validation for analysts' assumptions about operator behaviour. System operators can actually be observed during interaction with the accident simulation. Alternatively, analysts can use systems such as Prolog to answer queries about the course of an accident. For example, the following clauses provide information about the position of the Shift Leader at the first moment in time. The capital letter of Location is used to indicate a free variable that must be bound to an appropriate value in the result:
| ?- time(1, position(shift_leader, Location)). Location = line_office ?The following trace of interaction shows an attempt to find out if anyone had informed the Shift Leader about the sector fuel load. Here, the result tells us that they were told about this at time 2. It is important to note that Prolog could not identify the source of the information, Who. In our initial formalisation, the '_' was used to indicate that we did not know the source of the information. This accurately reflects the lack of evidence in the report itself:
|?- time(When, inform(Who, shift_leader, sector_fuel_load)). When = 2 ?Prolog is an example of a resolution proof system. Simulation is a by-product of this process. The technical details are less important here than an understanding that automated systems can be used to support the theorem proving process that was performed manually in Section 4.1. The complexity of this relatively simple proof indicates that manual theorem proving is a costly and error-prone task.
The first set of problems relate to the difficulty of constructing coherent temporal models for major accidents. It is a non-trivial task to resolve the contradictory timings that often appear in human factors and systems accounts. It can also be difficult to integrate imprecise temporal information about operator behaviour with the more precise temporal schemas that are available for process components It is important to stress that the development of coherent temporal models must not force analysts into arbitrary decisions or commitments to timings that are not supported by the available evidence. This paper has, however, argued that these errors and inconsistencies must be identified and then flagged within natural language accident reports. If this is not done then readers will continue to question the veracity of these documents that are intended to preserve the safety of future applications.
Usability concerns form the second set of problems that must be addressed during the temporal modelling of major accidents. We have argued that there may be an important trade-off between the visual appeal of temporal notations and the reasoning power that those formalisms offer to analysts and investigators. This is significant because formal proof techniques provide a powerful means of identifying the temporal ambiguities that have been criticised in the previous paragraph. Tool support has been identified as one means of improving the 'usability' of notations with a relatively low visual appeal. For example, Figure 22 shows how we have applied the three dimensional navigation facilities of VRML (Virtual Reality Markup Language) to address the scalability problems associated with fault trees and timelines.
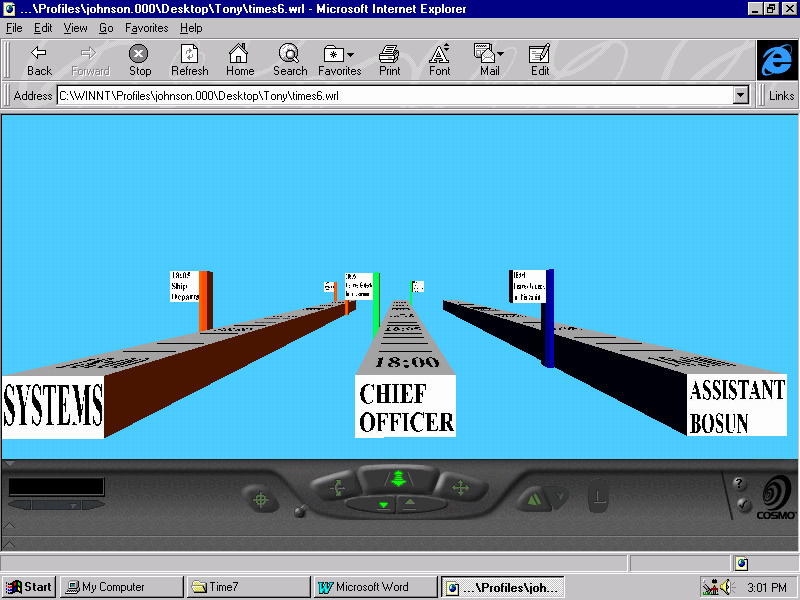
The final set of problems stem from the difficulties of managing cooperative work between heterogenous groups of experts. Rather than focusing on temporal expressiveness or visual appeal, these problems relate to aspects of control. For example, what are the consequences of allowing more than one author to simultaneously work on a formal or semi-formal description of an accident? Almost no research has been done into these issues. This is an important omission. Without some understanding of the group processes involved in accident modelling, it is unlikely that adequate tool support can be developed. This may explain why many existing systems, such as Fault-Tree editors, often only support specific areas of an accident investigation. They are frequently restricted to systems or control flow analysis. Few, if any, attempts have been made to support human factors investigations. The main argument in this paper has been that we must urgently address this lack of integration if we are to avoid the omissions, inconsistencies and errors that currently weaken most accident reports.
Thanks are due to the members of Glasgow Accident Analysis Group and the Glasgow Interactive Systems group (GIST) for valuable comments on an early draft of this paper. Tony McGill drove the development of the three dimensional time-lines shown in Figure 22.