Literate Specifications

Chris Johnson

Department of Computing Science,
University of Glasgow,
Email: johnson@dcs.gla.ac.uk

Abstract

The increasing scale and complexity of software is imposing serious burdens upon many industries. Formal notations, such as Z, VDM and temporal logic, have been developed to address these problems. There are, however, a number of limitations that restrict the use of mathematical specifications for large-scale, software development. Many projects take months or years to complete. This creates difficulties because abstract, mathematical requirements cannot easily be used by new members of a development team to understand past design decisions. Formal specifications describe what software must do, they do not explain why it must do it. In order to avoid these limitations, we propose a literate approach to software engineering. This technique integrates a formal specification language and a semi-formal design rationale. The Z schema calculus is used to represent what a system must do. In contrast, the Questions, Options and Criteria (QOC) notation is used to represent the justifications that lie behind development decisions. We then present empirical evidence which suggests that the integration of these techniques provides significant benefits over previous approaches to mathematical analysis and design techniques. The paper closes by describing a range of tools that have been developed to support our literate approach to the specification of large-scale software systems.

Introduction

Unfortunately, a number of limitations restrict the application of formal methods to support software engineering. Austin and Perkin's survey of four hundred and fourty-four commercial and academic software engineers provides detailed evidence about these weaknesses (Austin:93). The following table presents the percentage of respondents who felt that a number of issues were barriers to the commercial development of formal methods:

The specification is not readable by the clients. 		23%

Some aspects of specification are difficult to define 
in a mathematical model: timing constraints; HCI; 
performance;  reliability; maintainability; availability...	21%

A specification will not model all aspects of the real 
world: hardware; environment...					19%

Lack of experienced staff  					18%

To use a formal method you have to do proofs which 
dramatically increases the development time (and hence
cost)  								16%

Development costs increase  					15%

Mistakes can be made in the specification  			14%

From this analysis it is clear that many of the limitations of formal methods relate to the problems of communication. Mathematical specifications cannot easily be understood by clients. It is hard to train staff to develop specifications. It is difficult to avoid mistakes in specifications. Many of these problems stem from the fact that while formal specification techniques provide powerful means of representing the intended behaviour of a software system, they cannot easily be used to describe why that behaviour is appropriate. This prevents regulatory authorities, clients and other designers from understanding the motivation behind particular development decisions.

A number of further problems restrict the utility of formal methods for large-scale software engineering. Abstract, mathematical notations cannot easily be used to coordinate the activities of different development teams. This is a significant issue because team-based management structures are, typically, used to organise software development (Klein:93). These groups can be formed around specific sub-systems. Alternatively, they can be organised around different skill-bases; human factors groups must coordinate with systems engineering teams. In either case, many of the people in these teams will have little knowledge of discrete mathematics. This prevents them from understanding the implications that a formal specification may have for their development tasks. The use of a mathematical notation, therefore, jeopardises communication both within and between design teams (Johnson:95z). The extent of this problem has also been recognised by industry. Craigen, Gerhart and Ralston's international survey on the commercial application of formal methods concluded that there must be ``added emphasis on developing notations more suitable to use by individuals not expert in formal methods or mathematical logic'' (Craigen:93).

Design Rationale

Figure 1: The Structure of gIBIS diagrams.

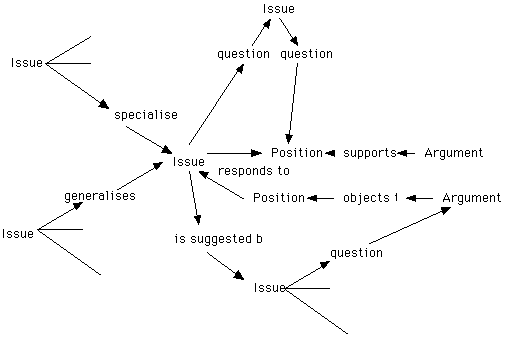
A limitation with this approach is that it can be extremely time consuming to develop models of the many different arguments that take place during software design meetings. gIBIS, therefore, involves considerable expense in terms of the recording process and in terms of the subsequent analysis. In contrast to the gIBIS approach, Figure 1 illustrates the simpler syntax of the Questions, Options and Criteria (QOC) notation (Shum:95).

Figure 2: A Simple QOC diagram.

These diagrams are built by identifying the key questions that must be addressed during the development of an interactive system. The options that answer a particular question can then by linked to it. Finally, the criteria that support those options are linked by either solid or dotted lines. The solid lines indicate supporting criteria. The broken lines indicate criteria that count against a particular option.

Design rationale offers a number of advantages for software development. Shum argues that semi-formal notations provide the flexibility that is required to represent the many different forms of decisions that have to made during the development life-cycle (Shum:91). A further advantage is that designers are not forced to learn complex syntax and composition rules (Johnson:95z). Klein argues that this the flexibility and informality of design rationale supports the communication of design decisions between the members of concurrent development teams (Klein:93). MacLean, Young, Bellotti and Moran regard the arguments that support decisions as the `co-products of design' (MacLean:91). If the justifications that support crucial decisions are explicitly represented then they can be shown to new members of development teams (Conklin:89). Yakemovic and Conklin argue that this helps to clarify the reasons for past development decisions (Yakemovic:90). Design rationale can also be shown to clients and regulatory authorities as part of the documentation for safety-critical software (Davies:85). It can help to demonstrate that sufficient attention has been paid throughout the development of large-scale software projects. This paper argues that these benefits must be recruited to support the use of formal methods in large-scale software development.

Not only is there an argument for supporting formal specifications with design rationale techniques. These is also a need to recruit the precision and rigour of mathematical specifications to support semi-formal notations, such as QOC and gIBIS. Design rationale lacks the precision that is required during the development safety-critical systems. For example, the natural language that is used to annotate QOC diagrams can easily be misinterpreted. Confusion often occurs when different development teams use the same terms to refer to different data items or sections of code. This can easily happen when QOC diagrams are produced without automated support for data dictionaries (Johnson:94). Semi-formal design rationale notations can also be inconsistent. This occurs if the same criterion is used both to support and weaken an option in different contexts (Johnson:95h).

In order for any integration of formal methods and design rationale to be successful it is critically important to minimise the additional burdens that will be placed upon the end-users of the technique. A frequent weakness of formal methods research is that it pays little regard to the software engineers who must eventually learn to apply their techniques (Johnson:95b). With this is mind, we have decided to exploit the QOC notation rather than the gIBIS design rationale. There are a number of reasons for this. The simpler syntax of the QOC notation makes it easier to construct and maintain than gIBIS diagrams. QOC also has a simpler semantics. It may, therefore, be easier to learn.

Literate Specifications

The argumentation in design rationale provides a means of communicating the findings of formal analyses to the members of concurrent design teams. The use of natural language within a graphical notation also provides the degree of flexibility that is necessary in order to communicate the justifications that lie behind particular design options. Formal specifications provide the degree of precision that is required by those who are responsible for programming an application.

Figure 3: Overview Of The Literate Specification Technique

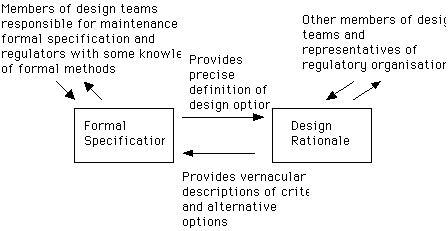
Figure 3 provides an overview of our approach to the literate specification of large-scale, software systems. Our proposed approach to the integration of design rationale and formal specification requires two additional forms of support if it is to be successfully used by `real-world' engineers on the development of `real-world' software. The first is empirical evidence that these techniques can be successfully used by today's generation of programmers and designers. We are, therefore, anxious to provide empirical evidence that demonstrates the `usability' of literate specifications. The second form of support for our approach is provided by the development of appropriate tools. This is a critical issue because 43\% of the respondents to Austin and Parkin's survey indicated that the lack of available tools were a significant barrier to the use of formal methods (Austin:93). Traditionally, formal methods research has focussed upon the provision of theorem provers and type checkers. In contrast, we are anxious to provide systems that support the communication of mathematical requirements and not simply their formal analysis or generation.

An Example Specification

The requirements for the control system can be briefly described as follows. Rupture accidents occur when contaminated primary coolant escapes from steam generator tubes into the containment. A warning system should detect contamination as coolant accumulates in sumps. An alarm should then be raised. The leakage will result in a fall in the level and pressure in the system's pressuriser. A reactor trip should then occur. Following this the operator must: establish a secondary heat sink; identify and isolate the faulty steam generator; cool and depressurize the primary coolant system; restore long term cooling. In order for safety to be preserved, designers must integrate the monitoring and detection systems with the user interface to the control applications. This is clearly a complex task given the many hundreds of variables that are sampled during coolant failures (Johnson:95z).

The rest of this section briefly introduces formal requirements for our example system. Readers who are more interested in the development of literate specifications than the details of our specification should move to the next section. The feedwater application can be described in terms of a number of parameters. The cntmnt_sump_level describes the depth of fluid in a containment sump. The pump_a_press represents the output pressure produced by pump A:

PARAMETER_IDS = {cntmnt_sump_level, pump_a_press,...}

Operations can be performed on the elements of PARAMETER_IDS. For instance, max and min values define a permissible range of values for each parameter. Automated systems and operators may request a new target value for a parameter; set:

__________Feed_System_Application______________________
|
| set, value, max, min: PARAMETER_IDS -> Z
| name: PARAMETER_IDS \fun TEXT
| user_input: power TEXT
| system_input: power TEXT
|_______
|
| forall p : PARAMETER_IDS o max(p) >= value(p) >= min(p)
|_____________________________________________________

The user interface to the feedwater control system requires the close cooperation of systems engineers and human factors experts. The former group must provide software and hardware to supply all necessary process information. The latter group must devise appropriate presentation techniques so that operators can read and understand the information which is presented to them. Requirements for both these groups can be represented using the abstractions of the Z specification language. For example, a sump_levels display can be used to represent information about the contamination of liquid accumulating within the drainage system. The image presented to an operator can be described in terms of a set of display formats:

DISPLAY_FORMATS = {sump_levels, steam_circuit,...}

______Feed_System_Display____________________________
|
| display_params: PARAMETER_IDS <-> DISPLAY_FORMATS
| display_text: TEXT <-> DISPLAY_FORMATS
| image: power DISPLAY_FORMATS
|____________________________________________________

Feed_System == Feed_System_Display ^ Feed_System_Application

An important requirement for our example system is that a warning is displayed if the system detects an attempt to set a variable below its authorised limit. The following schema provides a common focus for several different development teams. Software engineers must ensure that the system can detect and respond to a low setting. Human factors specialists must determine whether operators will actually be able to observe and understand the warnings specified in schemas such as Low_Set:

______Low_Set____________________________
|
| Xi Feed_System_Application
| Delta Feed_System_Display
| param? : PARAMETER_IDS
| new_setting? : Z
|--------------------------------
| new_setting? < min(param?)
|
| exists format : image' o
| (``Setting of " cat name(param?) cat`` low", format) in display_text'
| display_params' = display_params
| display_text' = display_text
|____________________________________________________

It is important to emphasise that mathematical specifications support communication between designers who have a clear understanding of the formal language. Discrete mathematics provides a vocabulary with clear semantics and well defined operators. Unfortunately, this strength can also be a weakness if other designers, clients and regulatory authorities only possess a limited knowledge of the formal language.

The Weaknesses Of Formal Methods

Lack Of Vernacular Descriptions

______User_Set_Response_______________________________________________
|
|Delta Feed_System
|param? : PARAMETER_IDS
|input_text? : TEXT
|text_to_num : TEXT -> Z
|
|-------------------------------------------
|
|exists format : image; setting : TEXT o
| (``Setting of " cat name(param?) cat``out of range", format) in display_text =>
| (input_text? = name(param?) cat setting) in user_input ^
| max(param) >= text_to_num(setting) >= min(param)
|
| system_input' = system_input
|
|____________________________________________________________________

This states that if a warning about an out of bounds setting for a process parameter is part of the displayed text then the user inputs a string that identifies the parameter and alters the setting to an admissible value.

Although this syntactic grouping helps to communicate the requirements that are represented in specifications, it does not provide a panacea for the use of formal methods within large development teams. It states what system software must do, it does not explain why it must do it. This problem can be avoided by using formal notations, such as deontic logics, to represent the arguments that support particular requirements. Unfortunately, this introduces further communications problems for designers who do not understand the mathematical notations that are used to represent the justifications behind formal requirements.

Figure 4: Linking Vernacular Argumentation And Formal Requirements

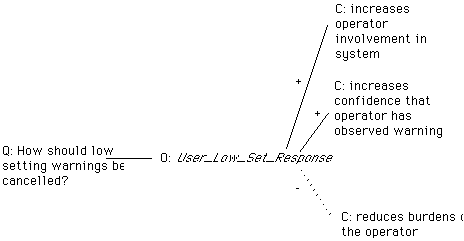
In contrast, our approach to the development of literate specifications avoids this problem by using vernacular and semi-formal argumentation structures to support the abstract requirements of formal methods. For instance, Figure 4 illustrates how a QOC rationale might be used to support the technique described in User_Set_Response. The requirement that users should provide input in response to the low setting warning is supported by the argument that this increases operator involvement. Designers may also be more confident that users will monitor their system and observe the warning if they are expected to actively intervene during control tasks. The formal requirement is not supported by the argument that this will reduce the burdens on the operator. It is important to emphasise that the formal schemas and semi-formal rationale are intended to be the co-products of our literate approach to specification. Although some training in discrete mathematics may still be required to understand the precise requirements in a formal specification, it is now possible for all members of a design team to question the arguments that support these formal assertions.

Lack Of Justification

______System_Set_Response_______________________________________________
|
|Delta Feed_System
|param? : PARAMETER_IDS
|input_text? : TEXT
|text_to_num : TEXT -> Z
|
|______________________________________
|
| exists format : image; setting : TEXT o
| (``Setting of " cat name(param?) cat`` out of range", format) in display_text=>
|(input_text? = name(param?) cat setting) in system_input ^
| max(param) >= text_to_num(setting) >= min(param)
|
|user_input' = user_input
|
|____________________________________________________________________

This states that if a warning about a low setting for a process parameter is part of the displayed text then the system inputs a string that identifies the parameter and alters the setting to an admissible value.

This lack of justification has important consequences for the application of formal methods. For instance, a development team might expect user confirmation of more serious problems, such as low pressure settings for pumping equipment. Automatic responses might be used for less important errors. Other designers within the same group or within different development teams cannot use schemas, such as User_Set_Response or System_Set_Response, to discover why an approach was appropriate in one context but not in another. In our example, it would be impossible for software engineers to reconstruct the implicit risk assessments that were used to select operator confirmation for low pressure settings. This makes it difficult for the same criteria to be applied throughout system development (Shum:94).

Our literate approach to specification is motivated by the need to explicitly represent the justification for particular requirements. Figure 5 illustrates this use of design rationale and formal methods.

Figure 5: Justifying Formal Requirements Using Design Rationale

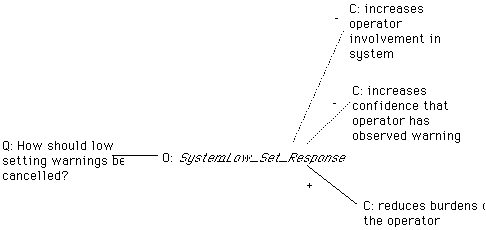
The requirements represented by System_Set_Response are justified by the argument that this reduces the burdens on system operators. These requirements are not supported by an increase in the designers' confidence that users will observe the warning. Nor are they supported by an increase in operator involvement. These justifications can be compared with those for User_Set_Response shown in Figure 5.

It is intended that these diagrams should be produced as a co-product of the formal development process. As various alternatives are assessed, the justification for each design option should be explicitly represented in a corresponding QOC diagram. It would then be possible to trace the reasons for adopting a particular requirement within a software system. It is important to acknowledge that there will be an additional overhead in developing both a design rationale and a formal specification. Following MacLean, Young, Belotti and Moran we argue that our integrated approach will repay any initial investment by ``(a) providing an explicit representation to aid reasoning about the design and the consequences of changes to it, and (b) serving as a vehicle for communication, for example, among the members of a design team or between the original designers and the later maintainers of a system.'' (MacLean:91).

Lack Of Status Information

______Remove_Set_Warning_______________________________________________
|
| Delta Feed_System
|
|----------------------------------------------
|
| exists warning_format : image, format : image' o
| ((``Setting of " cat name(param?) cat`` low", warning_format) in display_text ^
| ((input_text? = name(param?) cat setting) in system_input v
| (input_text? = name(param?) cat setting) in user_input) =>
| ((``Setting of " cat name(param?) cat`` low", format) not in display_text' |
|____________________________________________________________________

This states that if a warning about a low setting for a process parameter is displayed and the user or the system inputs a string that identifies the parameter and alters its setting then the warning is not displayed after that input operation.

It is important to emphasise that even more work is required before this schema can guide an implementation. For instance, it does not describe what should happen if concurrent input from the system results in another low setting at the same time as the previous warning is cleared. A further limitation is that it does not represent the real-time delays that may occur before the user or the system responds to the low setting. Again, there is no way of identifying the need for this further work from the formal specification. The lack of status information does not just cause problems for the refinement of software engineering requirements. Similar comments can be made about the device abstractions in previous schemas. They are not at a level of detail where a development team can proceed towards implementation. For instance, any number of sensors and monitors might be used to obtain process values. The selection of these devices will have a profound impact upon the anticipated frequency and granularity of process updates. Such factors will, in turn, have an impact upon the polling mechanisms that are used to sample the devices. These issues must be considered by both hardware and software engineers during the more detailed development of complex applications.

Many theoretical works on formal methods ignore the pragmatic problems that arise from the refinement of large-scale specifications (Morgan:90). There is an assumption that the level of detail will gradually increase in an almost uniform manner. Recent research into design practice has revealed that such assumptions are unwarranted (Johnson:95z,Klein:93). Less critical areas of a software system may be left at a high level of abstraction. More important areas and, in particular, those aspects that preserve safety must be considered in greater detail. Unless these areas can be agreed upon then development activities may be needlessly duplicated or omitted. This problem is exacerbated by the fact that different groups may be working on different areas within a specification. The lack of status information for abstract schemas, such as User_Set_Response, can prevent designers from coordinating and focusing their efforts upon those areas of a specification that require the most work.

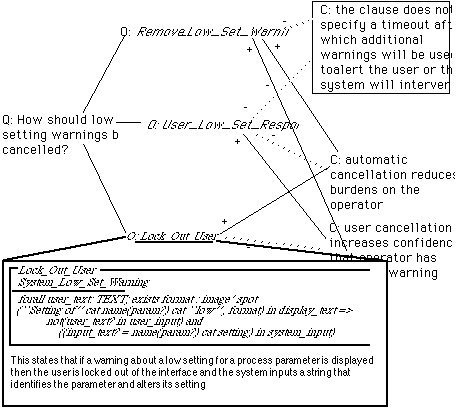
The integration of mathematical requirements and semi-formal, design rationale can be used to explicitly introduce status information into abstract specifications of large-scale systems. For instance, the Remove_Set_Warning schema can be criticised because it does not represent the duration of the delay that can arise before a user or the system responds to the low setting warning. This is unsatisfactory because at some point additional presentation resources may be required in order to direct the operator's attention towards the warning. Similarly, a time-out must be used to describe the maximum delay before system intervention. This need for further refinement can be indicated in design rationale by explicitly representing the status of particular schemas. By this we mean that QOC diagrams can be annotated to show those options that require further work. Figure 6 illustrates this technique.

Figure 6: Representing Status Information Using Design Rationale

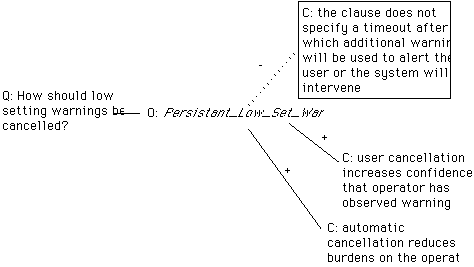
In this diagram, the option that the Remove_Set_Warning should be used to cancel the alarm is opposed by the observation that the schema does not consider the additional warnings which must be provided if the user does not observe the initial error display. Nor does it consider the time-outs that must be used in order to trigger system intervention. The use of the box around the criterion is not a standard part of the QOC syntax and is included to emphasise the need for further refinement. A number of benefits can be gained from this introduction of status information into formal specifications. In particular, it supports the use of mathematical requirements within concurrent engineering teams. For instance, schemas such as Remove_Set_Warning have implications both for systems engineers and for interface designers. The former group must implement the automatic time-outs. The latter group must devise appropriate presentation techniques to display the warning. By explicitly representing the status of this option both parties may recognise that this requirement needs further work. In this way, design rationale can provide a focus for the subsequent development of literate specifications.

Lack Of Alternatives

______Lock_Out_User_______________________________________________
|
|Xi System_Set_Response |
|------------------------------------------ |
|forall user_text : TEXT; exists format : image' o
| (``Setting of "cat name(param?) cat`` low", format) \in display_text =>
| not (user_text? in user_input) ^
| ((input_text? = name(param?) cat setting) in system_input)
|
|____________________________________________________________________

This states that if a warning about a low setting for a process parameter is displayed then the user is locked out of the interface and the system inputs a string that identifies the parameter and alters its setting.

The representation of rejected options is of critical importance during the subsequent development of large-scale software systems. Revisions to a set of initial requirements frequently force designers to re-consider the proposals that were discarded early in the development cycle. For instance, the decision to lock out the user might be rejected by regulatory and quality control groups. This is again illustrated by the events following the Three Mile Island Accident. The policy of minimal intervention was largely abandoned after problems in the North Anna reactor forced operators to intervene in order to preserve the safety of their system (Duncan:87b). Under such circumstances, designers might be forced to re-consider the option described by User_Set_Response rather than Lock_Out_User. As before, the integration of formal specification techniques and design rationale notations can be used to support this re-evaluation. For instance, Figure 7 exploits our extended QOC notation to represent alternative options for the confirmation of low setting warnings.

Figure 7: Representing Alternative Options Using Design Rationale

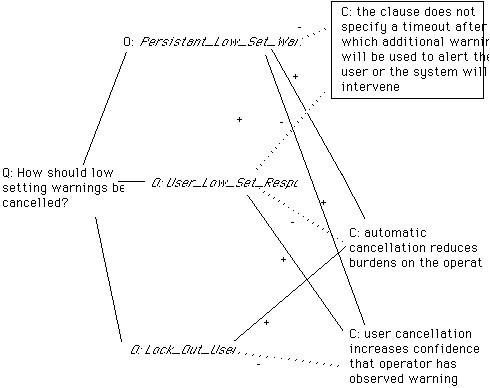
This diagram shows that a number of schemas might be represented as different design options within a QOC diagram. Software engineers might use this figure to reconstruct the arguments for and against user confirmation, automatic lock-outs and an approach that allows the system or the user to re-set parameters.

`Real-World' Support For Literate Specification

Figure 8: Qualitative Assessments Of Formal Methods

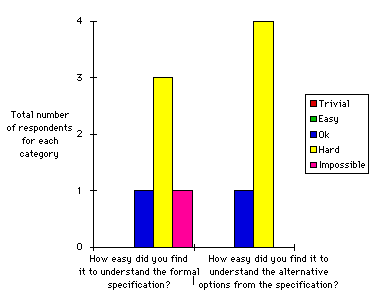
Such results are not particularly surprising. Formal methods are skill based activities. Clearly, one week's training is not sufficient to develop the expertise that is necessary to become confident in the use of mathematical specifications. Perhaps, more surprising are the qualitative responses for QOC diagrams. After being asked to analyse the Z specification, our subjects were shown a design rationale for another area of the chlorine recovery system. The results for the qualitative evaluation of QOC are shown in Figure 9.

Figure 9: Qualitative Assessments Of Design Rationale

In contrast to the formal specification, the subjects found it either trivial, easy or OK to understand the semi-formal notation. They also found it relatively easy to understand the design alternatives that were represented as options in the QOC. This evidence seems to back up the claims that were made for design rationale in the previous section. It is important to emphasise, however, that no direct comparisons can be made between the attitude statements in Figures 8 and 9. Clearly, the information content in the specification and the design rationale is quite different.

Finally, we presented the subjects with a literate specification that included both Z schemas and QOC diagrams. The results are shown in Figure 10. All of the subjects found that the integration of these techniques would be either useful or OK in their everyday work. This is an extremely encouraging finding considering the antipathy to formal methods that one frequently encounters amongst software engineers whose training has included only a minimal amount of discrete mathematics None of our subjects had any previous training in formal specification or discrete mathematics.

Figure 10: Qualitative Assessments Of Literate Specifications

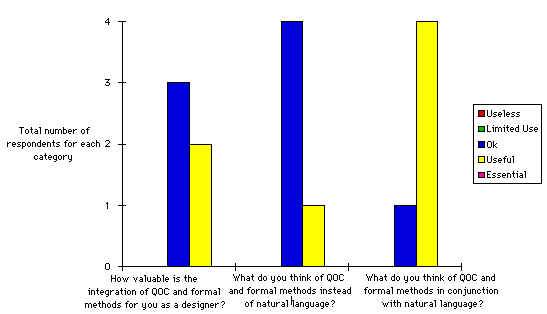
These findings are suggestive rather than conclusive. It is important not to under-estimate the difficulty of performing rigorous evaluations with practising engineers. We had to train our subjects over a significant period; this involved a high degree of commitment from both the individuals concerned and from their companies. We are currently attempting to replicate our results with larger groups of software engineers drawn from a wider range of companies. These investigations are discussed in more detail in a companion paper (Johnson:95lit).

Tool Support

Constructing And Maintaining Literate Specifications

Chan's tool can not only provides means of navigating QOC diagrams. It also provides a novel means of navigating through the schemas of a formal specification. The names of abstract requirements can be used to label the options in a QOC network. These can then be selected to reveal their full formalisation. This enables designers to directly view the different requirements in a literate specification by selecting the text shown in a QOC diagram. This approach is illustrated by Figure 11.

Figure 11: Storing Schemas As Hypertext Links In Chan's Tool

Chan's tool has important advantages over many existing systems for constructing and maintaining formal specifications. In some of these applications, it can be difficult for designers to visualise the ways in which schemas relate to each other. They are forced to go through many different displays in order to inspect the hundreds of different clauses that characterise non-trivial systems. In contrast, the QOCs of literate specification provide a powerful structuring mechanism for formal requirements. The semi-formal links between questions and associated criteria provide the contextual information that is necessary in order to understand large-scale specifications.

It is important also to emphasise that our tool has many weaknesses when compared with other formal specification systems. For instance, there is no type checking. There is no support for theorem proving. Other problems relate to the user interface. For instance, there are only rudimentary facilities for displaying mathematical symbols. It can be difficult to view schemas against a background of questions, options and criteria. Current work is extending the system through the use of colour as a redundant cue to the role of a schema within a specification. A further problem is that the tool provides little or no support for version control. This makes it difficult for designers to trace how literate specifications change during the development lifecycle. New members of existing design teams cannot easily use the tool to understand successive changes in the development of a software system.

Reasoning About The Structure Of Literate Specifications

Figure 12: The Potential For Contradiction In Design Rationale

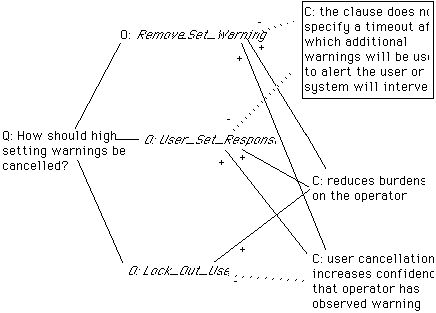
The formal requirement that the user explicitly acknowledges a high setting warning is supported by the criteria that this will reduce the burdens on the operator. This argument represents a potential inconsistency because in Figure 7 it was argued that an explicit acknowledgement did not reduce the burdens on the operator. There may be perfectly good reasons why a criteria is used in this apparently contradictory fashion. However, it is important that designers can explicitly identify these inconsistencies if they are to justify them before quality control groups and regulatory authorities. A second strand of research has, therefore, been developing Prolog based tools that can be used to reason about the structure and consistency of literate specifications. The following clauses illustrate this approach by representing the reasons for and against explicit user confirmation of low set warnings:

qoc(low_set_cancel, persistant_set_warning, low_burdens).
qoc(low_set_cancel, persistan_set_warning, confirms_observation).
qoc(low_set_cancel, user_set_response, not(low_burdens)).
qoc(low_set_cancel, user_set_response, confirms_observation).
qoc(low_set_cancel, lock_out_user, low_burdens).
qoc(low_set_cancel, lock_out_user, not(confirms_observation)).

qoc(hig_set_cancel, user_set_response, low_burdens)).

inconsistency(Ques1, Ques2, Opt, Crit):-
qoc(Ques1, Opt, Crit), qoc(Ques2, Opt, not(Crit)).

|?- inconsistency(low_set_cancel,Ques, Opt, Crit).

Ques = high_set_cancel 
Opt = user_set_response
Crit = low_burdens?

Uniting Graphical Interaction And Structural Reasoning

Figure 13: The Architecture Of The Prelog Tool

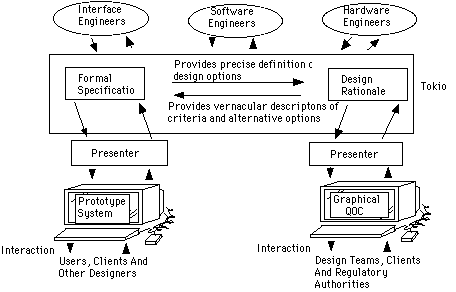
Prelog is built from two existing systems. The Tokio temporal logic interpreter is used to maintain the qoc clauses from the Prolog tool. This interpreter was chosen because elsewhere we have argued for the need to consider temporal properties in the development of safety-critical applications (Johnson:95c,Johnson:95z). The same article also considers ways in which Tokio can be used to rapidly derive partial implementations from abstract specifications. For now it is sufficient to observe that Tokio provides the same resolution techniques as those provided by Prolog and so it involves no additional overheads if designers simply want to use first order logic. Unfortunately, qoc clauses provide an extremely cumbersome means of constructing and viewing literate specifications. Fortunately, Prelog also provides access to the Presenter screen management system. This tool is used to directly translate the textual output of Tokio into the graphical form of the QOC notation. We have implemented our system in such a way that the logic clauses can be automatically generated from the graphical representation. This has the advantage that designers need never directly interact with qoc clauses.

It is important to emphasise that the development of tool support for literate specification is an area of on-going research. For example, we have yet to directly address the problems of maintaining conformance between a formal specification and its design rationale. If changes are made to a schema then surely the rationale ought to be updated to reflect that alteration? This is clearly a critical issue in the development of tool support. Our recent focus upon version control is helping to address this problem. Designers can chart the changes that occur within a specification and a QOC diagram. This is not a complete solution. For instance, the Prelog presentation of a QOC diagram might be altered to warn designers that modifications are required once the underlying specification has been changed. This raises a number of further issues that remain to be explored. For instance, introducing a new schema into a specification might have knock-on effects throughout many different areas of a design rationale. In our example, the introduction of a new option for the cancellation of warnings might affect the argumentation behind both high and low settings etc. At present there are no clear procedures or heuristics for tracking these knock-on effects.

Conclusion And Further Work

There are a number of areas for further work. Many of these have been mentioned in the previous sections of the paper. For instance, our tools must be improved to support version control mechanisms and type checking facilities. There are other areas that also remain to be explored. For example, Fischer, Lemke, McCall and Morch argue that it is possible to develop a large corpus of domain specific design rationale to guide the development of future systems (Fischer:91). This approach might be extended to support our use of QOC within literate specifications. Libraries of formal requirements and informal rationales might reduce the costs of future projects through the re-use of design documents. Such developments remain long term objectives. Further work is required to determine whether it is possible to represent more generic requirements in the formal components of our rationales. The examples that have been used to illustrate our techniques are highly specific to particular classes of safety-critical software.

It is important to stress that the use of mathematical specification techniques does not remove the need for traditional software engineering practices. Requirements elicitation is a necessary precursor to the application of formal methods. Programmers must still implement and test the systems that satisfy formal requirements. In this paper we have argued that literate specification techniques can be used to support these various stages of development. Requirements analysts, programmers and quality assessment teams can not only find out what a system should do but why it should do it. This argument suggests an extremely wide role for the use of formal methods in the software lifecycle. A number of colleagues in Glasgow, including Gilbert Cockton, Phil Gray and Steven Clarke, have begun to identify practical techniques for extending literate specifications in this way. In a recent publication, they have introduced the notion of `literate development'. This expands the links that we have developed between formal and semi-formal representations to include vernacular and informal annotations at a variety of different levels of detail. The intention is to directly support requirements engineering, task analysis and software testing (Cockton:95). This work is very much in its infancy but it promises to bridge some of the divides that currently prevent formal methods from being used in conjunction with existing software engineering practices.

Acknowledgements

References

• S. Austin and G.I. Parkin. Formal methods: A survey. Technical report, Division Of Information Technology And Computing, The National Physical Laboratory, Teddington, United Kingdom, 1993. Sponsored by the United Kingdom Department of Trade and Industry.
  
  
• Barringer:85a,
  H. Barringer, R. Kuiper, and A. Pnueli. Now you may compose temporal logic specifications. In ACM Symposium On The Theory Of Computing, pages 51--63, New York, United States of America, 1985. ACM Press.
  
  
• Bowen:94,
  J. Bowen and M. Hinchey. Formal methods and safety-critical standards. IEEE Computer, August 1993.
  
  
• Bowen:93,
  J. Bowen and V. Stavridou. Safety-critical systems, formal methods and standards. Software Engineering Journal, pages 189--209, July 1993.
  
  
• Carrington:94,
  D. Carrington and P. Stocks. A tale of two paradigms - formal methods and software testing. In Proceedings Of The Z Users Meeting. Springer Verlag, Berlin, Germany, 1994.
  
  
• Chan:94,
  T. Chan. A graphical tool to support the QOC notation. Technical report, Department of Computer Science, University of York, York, United Kingdom, 1994. M.Sc thesis.
  
  
• Cockton:95,
  G. Cockton, P. Gray, S. Clarke, and C. Johnson. Literate development. In Critical Issues For User Interfaces. Springer Verlag, Berlin, Germany, 1995.
  
  
• Conklin:89,
  J. Conklin and M.L. Begeman. gIBIS: A tool for all reasons. Journal Of The American Society For Information Science, pages 200--213, May 1989.
  
  
• Craigen:93,
  D. Craigen, S. Gerhart, and T. Ralston. An international survey of industrial applications of formal methods. Technical Report NISTGCR 93/626, U.S. Department of Commerce, National Institute Of Standards And Technology, Githersburg, United States of America, 1993.
  
  
• Davies:85,
  K.R. Davies. Techniques for the identification and assessment of major accident hazards. In J. Burgoyne, editor, The Assessment And Control Of Major Hazards, pages 289--308. Pergamon Press, Oxford, United Kingdom, 1985.
  
  
• Dix:91,
  A.J. Dix. Formal Methods For Interactive Systems. Academic Press, London, United Kingdom, 1991.
  
  
• Duncan:87b,
  K.D. Duncan. Fault diagnosis training for advanced continuous process installations. In J. Rasmussen, K. Duncan, and J. Leplat, editors, New Technology And Human Error, pages 209 -- 221. J. Wiley and Sons, New York, United States of America, 1987.
  
  
• Fischer:91,
  G. Fischer, A.C. Lemke, R. McCall, and A.HJ. Morch. Making argumentation serve design. Human Computer Interaction, 6(3 and 4):393--419, 1991.
  
  
• Johnson:93c,
  C.W. Johnson. A probabilistic logic for the development of safety-critical interactive systems. International Journal Of Man-Machine Studies, 39(2):333--351, 1993.
  
  
• Johnson:92d,
  C.W. Johnson. Specifying and prototyping dynamic human-computer interfaces for stochastic applications. In J.L. Alty, D. Diaper, and S. Guest, editors, People And Computers VIII, pages 233--248. Cambridge University Press, Cambridge, United Kingdom, 1993.
  
  
• Johnson:95h,
  C.W. Johnson. Documenting the design of safety-critical, user interfaces. Interacting With Computers, 1995. Accepted and to appear early in 1996.
  
  
• Johnson:95b,
  C.W. Johnson. The economics of interface design. In K. Nordby, P.H. Helmersen, D. Gilmore, and S.A. Arnesen, editors, Human Computer Interaction - Interact '95, pages 19--25, London, United Kingdom, 1995. Chapman And Hall.
  
  
• Johnson:95c,
  C.W. Johnson. Time and the web: Representing temporal properties of interaction with distributed systems. In M.A.R. Kirby, A.J. Dix, and J.E. Finlay, editors, People And Computers X, pages 39--50, Cambridge, United Kingdom, 1995. Cambridge University Press.
  
  
• Johnson:95z,
  C.W. Johnson. Using Z to support the design of interactive, safety-critical systems. IEE Software Engineering Journal, 10(2):49--60, 1995.
  
  
• Johnson:95lit,
  C.W. Johnson. Literate specification: Using design rationale to support formal methods in the development of human-machine interfaces. ACM Transaction on Human Computer Interaction, 11(4):291--320, 1996.
  
  
• GrayJohnson:95,
  C.W. Johnson and P. Gray. A critical analysis of interface specification notations. Technical Report TR-1995-6, Department of Computer Science, University of Glasgow, Glasgow, Scotland, G12 8QQ., 1995. Early Version Of Paper To Appear In The Second Eurographics Workshop On The Design, Specification And Verification of Interactive Systems.
  
  
• Johnson:94,
  C.W. Johnson, J.C. McCarthy, and P.C. Wright. Using a formal language to support natural language in accident reports. Ergonomics, 38(6):1265--1283, 1995.
  
  
• Kirkpatrick:81,
  M. Kirkpatrick and K. Mallory. Substitution error potential in nuclear power plant control rooms. In R.C. Sugarman, editor, Proceedings Of The 25th Annual Meeting Of The Human Factors Society, pages 163--167. Human Factors Society, Santa Monica, United States of America, 1981.
  
  
• Klein:93,
  M. Klein. Capturing design rationale in concurrent engineering teams. IEEE Computer, 26(1):39--47, 1993.
  
  
• Knuth:84,
  D.E. Knuth. Literate programming. Computer Journal, 27(2):97--111, 1984.
  
  
• MacLean:91,
  A. MacLean, R.M. Young, V.M.E. Bellotti, and T.P. Moran. Questions, options, and criteria: elements of design space analysis. Human-Computer Interaction, 6(3-4):201--50, 1991.
  
  
• MOD:91,
  Ministry Of Defence. Requirements for the Procurement of Safety Critical Software, MOD DEF-STAN 00-55, London, United Kingdom, 1991.
  
  
• Morgan:90,
  C. Morgan. Programming From Specifications. Prentice Hall, London, United Kingdom, 1990.
  
  
• Moszkowski:93,
  B. Moszkowski. Some very compositional temporal properties. Technical Report TR-466, Department of Computing Science, University of Newcastle Upon Tyne, Newcastle, United Kingdom, 1993.
  
  
• NASA:89,
  National Aeronautic and Space Administration. Advanced Orbiting Systems - Architectural Specification For The CCSDS Secretariat, Washington DC, United States of America, 1989.
  
  
• Pew:81,
  R.M. Pew, D.C. Miller, and C.E. Feehrer. Evaluating nuclear control room improvements through analysis of critical operator decisions. In R.C. Sugarman, editor, Proceedings Of The 25th Annual Meeting Of The Human Factors Society, pages 100--104. Human Factors Society, Santa Monica, United States of America, 1981.
  
  
• Sergot:95,
  M. Sergot. Applications of normative reasoning. In M. Harrison and P. Zave, editors, IEEE International Symposium On Requirements Engineering '95, page 98. IEEE Press, New York, United States of America, 1995.
  
  
• Shum:91,
  S. Buckingham Shum. Cognitive dimensions of design rationale. In D. Diaper and N.Hammond, editors, People And Computers VI: Proceedings Of HCI'91. Cambridge University Press, Cambridge, United Kingdom, 1991.
  
  
• Shum:95,
  S. Buckingham Shum. Analysing the usability of a design rationale notation. In T.P. Moran and J.M. Carroll, editors, Design Rationale Concepts, Techniques And Use. Lawrence Erlbaum, Hillsdale, New Jersey, United States of America, 1995.
  
  
• Shum:94,
  S. Buckingham Shum and N. Hammond. Argumentation-based design rationale: What use at what cost? International Journal of Human-Machine Studies, 40(4):603--652, 1994.
  
  
• Siu:91,
  N. Siu and C. Acosta. Dynamic event tree analysis - an application to SGTR. In G. Apostolakis, editor, Probabilistic Safety Assessment And Management, volume 1, pages 413--418. Elsevier, London, United Kingdom, 1991.
  
  
• Spivey:92,
  J.M. Spivey. The Z Notation: A Reference Manual. Prentice Hall, London, United Kingdom, 2 edition, 1989.
  
  
• Thimbleby:90a,
  H.W. Thimbleby. User Interface Design. Addison Wesley, Wokingham, United Kingdom, 1990.
  
  
• Yakemovic:90,
  K.C.B. Yakemovic and J. Conklin. Report on a development project use of an issue based information system. In Proceedings of CSCW'90: Computer Supported Cooperative Work, pages 105--118, New York, United States of America, 1990. ACM Press.