Figure 1: Literate Specification for the Warning Cancellation.
Accident reports are produced by regulatory and commercial authorities, such as the UK Air Accident Investigation Branch and the US National Transportation Safety Board, in response to most major accidents. These documents are intended to ensure that disasters do not recur. They, typically, contain accounts of the human and system failures that lead to major accidents. These descriptions are then used to identify the primary and secondary causes of the failure. Finally, recommendations are made so that the operators and regulators of safety-critical systems can avoid future accidents. Unfortunately, it is often difficult for readers to trace the way in which particular conclusions are drawn from the many hundreds of pages of evidence in these reports. Natural language arguments often contain implicit assumptions and ambiguous remarks that prevent readers from understanding the reasons why a particular conclusion was drawn from a particular accident. In contrast, this paper argues that mathematical proof techniques can be used to support the findings of accident investigations. These techniques enable analysts to formally demonstrate that a particular conclusion is justified given the evidence in a report. The later sections of this paper then introduce Conclusion, Analysis and Evidence diagrams. These can be used to communicate the results of a formal analysis. The intention is not to replace the natural argumentation structures that are currently used in accident reports. Rather, our aim is to increase confidence that particular conclusions are well supported by the evidence that is presented within a report.
The Mount Ymitos was outbound from the Mississippi River en route to St Petersburg, Russia. It had cleared the Southwest Pass out of the River when the Third Officer noticed an inbound passenger vessel using their binoculars. At this stage, he estimated that the vessel was approximately six miles from the Ymitos. He did not immediately report his observation as the Captain was busy with the Pilot who was preparing to leave the Mount Ymitos. The watch-standers re-established visual contact when the Noordam had closed to two miles from the Mount Ymitos. The Captain reduced their speed to dead slow and expected the Noordam to alter its heading. At this point the ARPA (Automatic Radar Plotting Aid) showed that the closest point of approach was under six hundred feet. The Captain made several attempts to alert the Noordam. At 20:40:08 the Coast Guard logged a Channel 16 VHF call: 'Passenger Vessel, Passenger Vessel, Go to South Pass'. At 20:40:50 they logged 'Passenger Vessel Going to South Pass, I Turn Hard Starboard'. The third officer then attempted to communicate the warning using an Aldis lamp. No response was received.
The Noordam was en route to New Orleans from Cozumel, Mexico. At approximately 20:00:00, Second Officer Smit called the Pilot Station and learned that two other vessels were also in-bound towards the Mississippi and could be overtaken. The Pilot did not alert the Noordam to the presence of any outward bound vessels. Quartermaster Salyo was the designated lookout He left the bridge on two separate occasions during the approach. Shortly after 20:00:00 he left, with the permission of Second Officer Smit, to make sandwiches and coffee for the bridge crew. At 20:10:00 he unlashed the anchors in preparation for entering port. He returned at 20:20:00 but did not detect the Mount Ymitos until immediately prior to the collision. A scheduled watch change took place at 20:30:00. Second Officer Smit performed navigation checks using the radar, together with Chief Officer Broekhoven, before handing over to Third Officer Veldhoen. Veldhoen, in turn, handed over to the Chief Officer at 20:36:00 when an 'end of sea voyage' was declared. This is a point of convenience determined by the watch officer and represents the point at which the Chief Officer assumes control for the manoeuvring watch prior to arrival in port. In order to complete this hand-over Veldhoen had to fix the vessel's position, complete the log and notify the engine room. As the Noordam changed course to enter the final leg of the approach, Fourth Officer Kuiper, who was on the bridge but who was not on duty, saw the lights of the Mount Ymitos and immediately issued a curse. The manoeuvre was halted while the crew determined the course and position of the vessel that they had seen, Approximately one minute before the collision, Chief Officer Broekhoven ordered left full rudder to pull away from the danger.
The Coast Guard's report argues that the principle reason for the collision was the failure by the Noordam's crew to keep an adequate watch. Unfortunately, the report does not provide a detailed explanation of why this failure occurred. The reader is left to infer the causal relations that link the observations about the accident and the conclusions that are listed at the end of the document. The following pages, therefore, show how formal techniques can be used to explicitly link the findings of an investigation to the account of an accident.
"Fourth Officer Daniel Kuiper, who was not on duty, was the first to notice the lights of a vessel off the starboard side of the Noordam. This was between one and two minutes before the time of collision. He saw a red light that he estimated was approximately 2 points off the NOORDAM's starboard bow - a point being 11.25 degrees of arc. First Officer Kuiper uttered a curse word that attracted the attention of others on the bridge. Third Officer Veldhoen, upon looking to starboard, also saw lights." [Paragraph 42]
Additional information, such as the conversion between points and degree of arc, is included to help the reader form a picture of the accident. Unfortunately, such details may actually obscure the underlying causes of operator 'error' and system 'failure'. Our previous work on accident analysis has, however, identified a number of categories that can be used to identify critical components in an accident:
| Physical Locations | Roles | Information/Control Systems |
| captain_veniamis | lookout | arpa_radar |
| pacific_trident | chief_officer | visual |
| mount_ymitos | first_officer | binoculars |
| noordam | third_officer | - |
| - | fourth_officer | - |
| - | watch_officer | - |
| Operators | Speech Acts | Tasks |
| pilot_station | inbound_pacific_trident | navigation_radar_check |
| engine_room | inbound_captain_veniamis | collision_radar_check |
| smit | outbound_mount_ymitos | correlate_radar_targets |
| salyo | curse | declare_end_of_sea_voyage |
| broekhoven | take_bearing_on_lights | fix_vessel_position |
| veldhoen | lights_moving_right | complete_log |
| kuiper | officer_change | notify_engine_room |
| - | - | end_of_sea_voyage |
| - | - | left_full_rudder |
Table 1: Critical Entity Table for the Noordam Accident
In formal terms, the elements of this table define the types that model the Noordam accident. The process of building such a table helps to strip out irrelevant detail that obscures critical properties of major accidents.
role(chief_officer, broekhoven). (1) role(first_officer, smit). (2) role(third_officer, veldhoen). (3) role(lookout, salyo). (4)Such clauses gather together information that is, typically, scattered throughout conventional, natural language documents. The roles performed by key individuals in the Coast Guard's report are listed in paragraphs [13, 16, 25, 30, 37, 42]. Such a formalisation is also important if an individual's role changes during the course of an accident. For example, the officer in charge of the watch on the Noordam changed at 20:30 hrs:
at(role(watch_officer, smit) , 2029). (5) at(role(watch_officer, veldhoen) , 2030). (6)The previous clauses exploit a simple form of temporal logic in which the binary at operator takes a proposition and a term denoting a time such that at(p, t) is true if and only if p is true at t. A number of technical problems surround the general application of this simple extension to propositional logic. In particular, the philosophical issue of reification forces analysts to clearly state the relationship between particular terms and objects over time. This theoretical problem is less of an issue for our purposes because we are always refering to definite entities at specific times during an accident. We, therefore, retain this simple temporal framework rather than the more elaborate temporal languages in our previous work (Johnson, 1993, 1995a, Telford and Johnson, 1996).
exists t: at(message(pilot_station, smit, inbound_captain_veniamis), t).(7) exists t: at(message(pilot_station, smit, inbound_pacific_trident), t). (8)The existential quantifier (read as 'there exists') is used because the accident report does not represent the precise times associated with each of these individual communications. The following clause shows how the same approach can be adopted to represent a lack of communication. Smit did not receive information about outbound traffic from the Pilot Station:
forall t: not at(message(pilot_station, smit, outbound_mount_ymitos), t).(9)The universal quantifier (read as 'for all') is used because it was never the case that Smit received information from the Pilot Station about the Mount Ymitos. Similar clauses can be used to represent more complex verbal exchanges. For example, Kuiper first observed the Ymitos' lights and issued a curse which was heard by Veldhoen and Broekhoven. Broekhoven then requested that Veldhoen take a bearing on the lights. Veldhoen responded that the lights were moving right. The following clauses represent these individual speech acts:
exists t, t' : at(message(kuiper, [veldhoen, broekhoven], curse), 2040) ^ at(message(broekhoven, veldhoen, take_bearing_on_lights), t) ^ at(message(veldhoen, broekhoven, lights_moving_right), t') ^ after(2040, t) ^ after(t, t'). (10)It is important to note that the preceding clauses do not represent the precise verbal components of each speech act. This information could be introduced if it were available, for instance through studying cockpit voice recordings. In the case of the Noordam there was no such record. Place holders, such as curse, are used to capture the recollected sense of the communication without specifying its exact form.
at(position(salyo, galley(noordam)), 2000). (11) at(position(salyo, bridge(noordam)), 2010). (12) at(position(salyo, decks(noordam)), 2015). (13)The previous clauses do not specify the relative position of the galley, bridge or decks. Such information can be introduced by formalising a three-dimensional co-ordinate scheme (Johnson, 1996). This was not done because clauses (11,12,13) reflect the level of detail in the Coast Guard's report. This illustrates an important benefit of the formalisation. Logic provides an explicit representation of the level of abstraction that is considered appropriate for the readers of the report. They do not need to know the relative positions of the galley, bridge and decks in order to understand the events leading to the collision. Such decisions are extremely important. Too much detail and readers will be swamped amongst a mass of contextual information. Too little detail and it will be difficult for them to reconstruct the flow of events leading to disaster. Clauses, such as (11,12,13), can be used to represent and reason about appropriate levels of abstraction. This helps to avoid the ad hoc decisions that frequently seem to be made about the amount of location information that is included in accident reports (Johnson, McCarthy and Wright, 1995).
"Between 2030 and 2036, Broekhoven and Veldhoen checked the radars occasionally, using the six mile scale. Broekhoven was planning the turn from 325 degrees to 000 degrees to coincide with bringing the Racon 'T' platform abeam, at 1.5 miles to port. Both Veldhoen and Broekhoven used the 10-centimetre and centimetre radars to check the distance of the domino platforms, and particularly the bearing and range of the Racon 'T'. They were not using the radars for collision avoidance and observation of moving targets, and did not attempt to correlate every fixed target contact in the radar with fixed platforms observed visually to see if any were any underway contacts rather than fixed platforms." [Paragraph 39]
From this it is possible to extract two critical observations about the operation of the Noordam. Firstly, that between 20:30, and 20:36 both Broekhoven and Veldhoen were performing navigation radar checks. Secondly, that during this interval they did not correlate radar targets with visual observations. The following clauses introduce a during operator such that during(p, t) is true if and only if the situation denoted by p occurs at sometime during the interval denoted by t. Formally, this can be given as follows:
forall t : during(p ,t) <=> exists t' : at(p, t') ^ before(t', end(t)) ^ before(begin(t), t').(14)This assumes that before(t, t') is true if t' occurs at some time after t or at the same instant as t. The following clauses also introduce the operator, in, such that in(t, t', t'') is true if t is wholly contained within t' and t''. This can be formalised in a similar manner to during. In contrast, the following clauses formalise the observations made in paragraph [39] of the accident report:
exists t : during(perform(broekhoven, navigation_radar_check), t) ^ not during(perform(broekhoven, correlate_radar_targets), t) ^ in(t, 2030, 2036). (15) exists t : during(perform(veldhoen, navigation_radar_check), t) ^ not during(perform(veldhoen, correlate_radar_targets), t) ^ in(t, 2030, 2036). (16)An important benefit of the formalisation process is that clauses, such as (15) and (16), can be translated back into natural language sentences; between 20:30 hrs and 20:36 hrs Broekhoven and Veldhoen performed navigation radar checks but did not correlate radar targets. The formalisation process helps analysts to focus upon critical aspects of an accident, such as operator tasks. This benefit might be obtained using a conventional task analysis technique such as TAKD (Johnson, Diaper and Long, 1984). Later sections will, however, argue that formal reasoning techniques can be used to prove properties of accident reports. This provides the additional degree of assurance that is demanded by bodies such as NASA and the UK Ministry of Defence (Austin and Parkin, 1993).
The previous example describes a relatively simple set of observations about operator tasks. Typically, the co-ordination of group activities is more complex. For example, Veldhoen declared an 'end of sea voyage' between 20:34 and 20:38. This procedure handed over control of the watch to the First Officer Broekhoven. He was responsible for navigating the Noordam into port. This change was not, however, announced to the lookout:
exists t : during(perform(veldhoen, declare_end_of_sea_voyage), t) ^ not during(message(broekhoven, salyo, officer_change), t) ^ during(role(watch_officer, broekhoven), t) ^ in(t, 2034, 2038). (17)The failure to inform the lookout was important because the task of declaring the 'end of sea voyage' involves the watch officer in a number of sub-tasks that reduce the amount of time that they have available for navigation and collision avoidance:
forall t: during(perform(veldhoen, declare_end_of_sea_voyage), t) <=> during(perform(veldhoen, fix_vessel_position), t) ^ during(perform(veldhoen, complete_log), t) ^ during(message(veldhoen, engine_room, end_of_sea_voyage), t). (18)Such clauses illustrate how the products of hierarchical task analysis might be introduced into formal models of major accidents. The higher order task of declaring the 'end of sea voyage' is comprised of three sub-tasks: fixing the vessel's position; completing the log and notifying the engine room.
exists t : at(observe(veldhoen, mount_ymitos, visual), t). (19) forall t : not at(observe(veldhoen, mount_ymitos, azimuth), t). (20)As before, the existential quantifier is used in clause (19) because the accident report does not identify the particular interval when Veldhoen made his observation. All we know is that there exists a time at which Veldhoen made a visual observation of the Ymitos. The universal forall quantifier is used in clause (20) because Veldhoen did not use an Azimuth circle at any time in the accident. This shows how an analysts concerns can direct the formalisation process. Clause (20) represents something that the officer did not do. If it had not been formalised then readers would not have been aware of this omission. In fact, Veldhoen's failure to verify his visual observations reinforced Broekhoven's judgement that the ships would pass starboard to starboard. He had seen a green (starboard) light shortly after the initial observation made by Kuiper:
exists t :
at(observe(broekhoven, green_light(mount_ymitos), binoculars), t).(21)
It was only when Broekhoven saw a red light that he realised the imminent possibility of a collision with
the Mount Ymitos and took evasive action:
at(observe(broekhoven, red_light(mount_ymitos), visual), 2041) ^ at(message(broekhoven, engine_room, left_full_rudder), 2041). (22)This section has used temporal logic to formalise the events leading to an accident. This formalisation process helps to strip out the contextual detail that hides critical observations in the many hundreds of pages that form conventional reports. We have not, however, shown that this approach can be used to reason about the conclusions that are drawn from an accident report.
'The proximate cause of the casualty was the failure of Chief Officer Broekhoven, the person in charge of the watch on the NOORDAM at the time of the casualty, to maintain a vigilant watch in that he did not detect the presence of the MOUNT YMITOS visually or on radar until the MOUNT YMITOS was less than 1 mile away, less than 2 minutes before the collision.' [Conclusion 1].
Such findings create a number of problems for organisations that must prevent the recurrence of future accidents. In particular, it does not explain the reasons why Broekhoven failed to spot the Mount Ymitos. Readers are left to piece together or infer these justifications from the evidence presented in the many previous pages of analysis. This can have extremely serious consequences. Two readers might easily infer two different reasons why Broekhoven failed to keep an efficient watch. Each might, therefore, adopt quite different strategies for avoiding future failures (Reason, 1990).
Formal proof techniques can be used to demonstrate that a conclusion is valid given the evidence that is presented in an accident report. For instance, the following clause is derived from Conclusion 1 in the Coast Guard report:
forall t: not during(vigilant(broekhoven), t) <=> not( during(observe(broekhoven, mount_ymitos, visual), t) v during(observe(broekhoven, mount_ymitos, arpa_radar),t)) ^ before(t, 2040). (23)We can re-write this clause as follows:
<=> not during(observe(broekhoven, mount_ymitos, visual), t) ^ not during(observe(broekhoven, mount_ymitos, arpa_radar),t) ^ before(t, 2040). [DeMorgan's Law (23)] (24) <=> (not during(observe(broekhoven, mount_ymitos, visual), t) ^ before(t, 2040)) ^ (not during(observe(broekhoven, mount_ymitos, arpa_radar), t) ^ before(t, 2040)). [^ Identity (24)] (25)In order to justify Conclusion 1 we must consider two different cases. The first concerns the reasons why Broekhoven failed to make visual contact with the Mount Ymitos. The second addresses the failure to detect the Ymitos using the ARPA radar. In order to establish the connection between the conclusion and the evidence presented in the body of the report it is necessary for analysts to explicitly state the reasons supporting particular findings. For example, one of the reasons why Broekhoven failed to observe the Mount Ymitos was that he used the radar for navigation and not for collision avoidance:
forall t: not during(observe(broekhoven, mount_ymitos, arpa_radar), t) <= during(perform(broekhoven, navigation_radar_check), t) ^ not during(perform(broekhoven, correlate_radar_targets), t). (26)We can now prove that the second part of our formalisation of Conclusion 1 is satisfied by the evidence in the accident report. This can be done by applying the following inference rule to (15) and (26).
forall t: P(t) => Q(t), exists t': P(t') |- exists t': Q(t') (27)Informally, this argument can be expressed as follows. From clause (26), we conclude that Broekhoven failed to observe the Mount Ymitos using the ARPA radar during any interval in which he was performing a navigation radar check and did not correlating radar targets. From clause (15) we know that know that Broekhoven was performing a navigation radar check and was not correlating radar targets between 20:30 and 20:36. Clause (27) tells us that if, we have clause (26) and clause (15) we can infer that Broekhoven failed to observe the Mount Ymitos using the ARPA radar during the interval between 20:30 and 20:36.
The previous proof illustrates a weakness in the accident report. Our formalisation of Conclusion 1 stated that Broekhoven did not observe the Mount Ymitos using the radar until 20:42. Our model has been used to prove that Broekhoven was pre-occupied with navigation checks between 20:30 and 20:36. This leaves at least six minutes unaccounted for. During that time, Broekhoven began turning the Noordam to the North. The accident report makes no reference to the use of the ARPA during this interval. The reader has to assume that the system was not used during this or subsequent operations prior to the collision at 20:42. Such findings are significant because they have important consequences for the recommendations that might be drawn from the report. For example, it is normal practice for officers to correlate radar targets when approaching an unfamiliar port. In the interval from 20:30 to 20:36 we can clearly see that navigation problems explain why Broekhoven did not perform these checks. We cannot, however, explain the omission during the final six minutes before the collision.
The second part of Conclusion 1 states that Broekhoven did not make any visual observation of the Mount Ymitos until 20:42. The justification for this finding can be found in a subsequent conclusion, rather than in the body of the accident report:
'The number of personnel (both watch-standing and non-watch-standing) on the bridge of the NOORDAM between 2020 and the time of the collision may have raised the complacency level and lowered the attentiveness of the bridge watch-standers with regards to maintaining a dedicated visual and radar watch.' [Conclusion 5].
The evidence for this conclusion can be found in paragraph [41] which states that:
'There were seven other persons on the bridge of the NOORDAM at this time (20:37hrs) in addition to the chief officer, who was in control of the vessel - three other licensed officers (one on duty, and two off duty), one cadet, two quartermasters and the chief officer's wife' [Paragraph 41].
This led to considerable confusion during our analysis of the report. We initially identified eight, and not seven, other individuals on the bridge in the final minutes before the collision. This confusion arose because Salyo was identified both by his name and by his role as Quartermaster In order to form this association, the reader must remember the allocation of responsibilities that was introduced in paragraph [25] when reading paragraph [41]:
forall t: not during(observe(broekhoven, mount_ymitos, visual), t)<= during(position(kuiper, bridge(noordam)), t) ^ during(position(veldhoen, bridge(noordam)), t) ^ during(position(helmsman, bridge(noordam)), t) ^ during(position(chief_officers_wife, bridge(noordam)), t) ^ during(position(quartermaster_1, bridge(noordam)), t) ^ during(position(quartermaster_2, bridge(noordam)), t) ^ during(position(cadet, bridge(noordam)), t) ^ during(position(broekhoven, bridge(noordam)), t). (28)Paragraph [41] suggests that there were nine people on the bridge at 20:37:
at(position(kuiper, bridge(noordam)), 2037). (29) at(position(veldhoen, bridge(noordam)), 2037). (30) at(position(helmsman, bridge(noordam)), 2037). (31) at(position(chief_officers_wife, bridge(noordam)), 2037). (32) at(position(quartermaster_1, bridge(noordam)), 2037). (33) at(position(quartermaster_2, bridge(noordam)), 2037). (34) at(position(cadet, bridge(noordam)), 2037). (35) at(position(broekhoven, bridge(noordam)), 2037). (36)We can apply our definition of during, given in clause (14), to re-write each of the clauses from (29) to (36) in the following form:
exists t: during(position(kuiper, bridge(noordam)),t) ^ before(2037, end(t)) ^ before(begin(t), 2037). [Application of (14) to (29)] (37)By repeating the application of (14) in the manner described above, we obtain the following:
exists t : during(position(kuiper, bridge(noordam)), t) during(position(veldhoen, bridge(noordam)), t) ^ during(position(helmsman, bridge(noordam)), t) ^ during(position(chief_officers_wife, bridge(noordam)), t) ^ during(position(quartermaster_1, bridge(noordam)), t) ^ during(position(quartermaster_2, bridge(noordam)), t) ^ during(position(cadet, bridge(noordam)), t) ^ during(position(broekhoven, bridge(noordam)), t) ^ before(2037, end(t)) ^ before(begin(t), 2037). [Introduction of ^ from application of (14) to (29..36)] (38)Finally, by applying inference rule (27) we get the following clause which corresponds to the second condition in Conclusion 1. In other words, the derivation of the following clause formally proves that our conclusions are consistent with the information contained in the body of the report:
exists t : not during(observe(broekhoven, mount_ymitos, visual), t) ^ before(2037, end(t)) ^ before(begin(t), 2037). [Application of (27) to (28) using (38)] (39)This proof helps to identify a further problem with the Coast Guard report We have previously cited Conclusion 5 which states that the number of personnel on the bridge between 20:20hrs and the time of the collision may have lowered the attentiveness of Broekhoven with regards to maintaining a visual and radar watch. Our formal analysis reveals that the evidence for this assertion only applies to the interval from 20:37hrs until the time of the collision. This poses a number of problems. We do not know why Conclusion 5 mentions 20:20hrs rather than 20:37hrs as stated in the body of the report. It can only be speculated that a number of people arrived on the bridge at this time earlier time. Alternatively, if additional crew members gradually were arriving from some time before 20:20hrs then we do not know why this was chosen as the critical moment at which collision avoidance tasks were impaired.
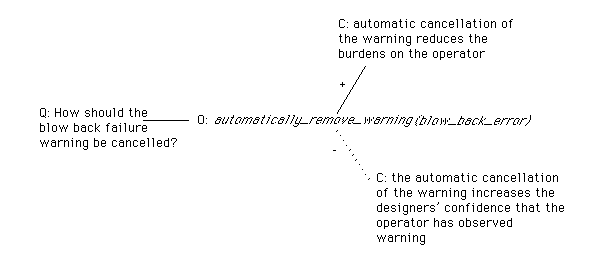
forall t , exists t': at(automatically_remove_warning(blow_back_error), t') <= at(state(blow_back, failed), t) ^ at(display(blow_back_error_icon), t) ^ at(system_cancel(blow_back_error_icon), t') ^ before(t, t'). (40)In previous papers, we have addressed these problems by developing literate specification techniques (Johnson, 1996a, 1996b). This approach uses the semi-formal argumentation of design rationale to support the use of formal methods during the systems development. Figure 1 illustrates this approach. Rank Xerox's Questions, Options and Criteria (QOC) notation is used to document the reasons why the previous clause might be adopted within the design of a particular system. QOC diagrams are built by identifying the key questions that must be addressed during the development of an interactive system (Buckingham Shum, 1995). The options that answer a particular question are then linked to it using the lines shown in Figure 1. Finally, options are linked to the criteria that support them, using solid lines, or weaken them, using broken lines. In Figure 1, the question of how to cancel blow-back warnings is answered by the design option that is specified by clause (40). This approach is justified by the criteria that the automatic cancellation of warnings reduces burdens on system operators. It is not supported by the criteria that this helps the operator to observe the warning. The diagram shown in Figure 1 is relatively simple in that it only shows a single option for the design question. In practice, these diagrams tend to show a number of alternative clauses each of which represents a different design option for the problem being considered. The interested reader is directed to Johnson (1996b) for more detail on the application of this approach.
Figure 1: Literate Specification for the Warning Cancellation.
This blend of formal and semi-formal notations can also support the formal analysis of accident reports. Natural language annotations of the Questions and Criteria provide non-formalists with an entry-point into the clauses that represent particular Options. In literate specification, these annotations provide the justifications for and against formal design requirements. In accident analysis, they link source material to the clauses that describe the relationship between evidence and conclusions.
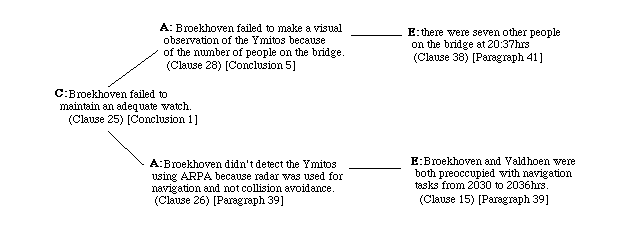Figure 2: Conclusion, Analysis, Evidence (CAE) Diagram for the Noordam Collision
There is an important difference between Conclusion, Analysis and Evidence diagrams and the Question, Options and Criteria notation. Options represent alternative design choices in QOC. In contrast, the analysis components of a CAE diagram support a single conclusion. They are not mutually exclusive. It should also be noted that the evidence shown in Figure 2 supports the analysis. It is possible to use dotted lines and '-' signs to indicate evidence which might contradict a particular line of enquiry.
CAE diagrams are not intended to replace the formal proof techniques that are used in their construction. The vernacular labels that represent the conclusions, analysis and evidence are open to the same problems of inconsistency and mis-interpretation that weaken the use of natural language in accident reports. For instance, it is perfectly possible to link a conclusion to a line of analysis that has little or no relationship to the conclusion. The use of formal proof techniques helps to ensure that this does not happen. It should also be emphasised that none of the techniques presented in this paper are intended to replace the use of natural language in accident report. Our use of discrete mathematics is similar to that of forensic scientists who frequently use continuous mathematical models, for instance of combustion. Both sorts of model can be used to represent and reason about the events leading to failure.
Figure 3: Conclusion, Analysis and Evidence diagram Integrating Formalisation and Informal Material
The United Kingdom Engineering and Physical Sciences Research Council has recently funded a three year investigation into the integration of formal reasoning and Conclusion, Analysis and Evidence diagrams for accident reports. We are particularly concerned to provide tool support for these techniques. For example, Figure 3 illustrates how CAE diagrams can be extended to represent the clauses that are used within the proof of a conclusion. This illustrates the mathematical relationship between the underlying evidence, at the bottom of the diagram, and the higher level conclusions. The task of constructing and maintaining such diagrams for complex accidents clearly requires some form of tool support, especially when one realises that key components of the proof, such as clause (27), are not shown. This problem could be addressed by exploiting hierarchical, graphical representations of formal proofs, such as tableaux . Hypertext display strategies might also be used to filter out the associated prose, or conversely, the mathematics at different stages during the analysis (Johnson, 1996b).
It is important to emphasise that CAE diagrams and formal proof techniques are not intended to replace the natural language presentation of accident reports. In contrast, our intention is to provide a clear and coherent structure for the argumentation in accident reports (Reason, 1988). This additional degree of precision is required if companies are to use these documents as a means of guiding future development and investment decisions.